机器学习基础(1)-机器学习概论
机器学习分类
机器学习范围宽泛、内容繁多。我们可以从多个角度对机器学习进行分类。
基本分类
机器学习的基本分类包括监督学习、无监督学习、强化学习,还可以包括半监督学习,主动学习。
监督学习(supervised learning)是指从标注数据中学习模型的机器学习。在监督学习中,有一些重要概念,分别是输入空间、特征空间和输出空间。输入与输出所有可能取值的集合被称为输入空间和输出空间。对于模型来说,每个具体的输入是一个实例,通常由特征向量来表示,而所有特征向量存在的空间称为特征空间。特征空间中,每一维对应一个特征。模型实际上都是定义在特征空间上的。有时候,输入空间和特征空间为相同的空间;而有时候,则需要将输入空间映射到特征空间。
监督学习的目的在于学习一个由输入到输出的映射,这一映射由模型来表示。监督学习的模型可以是概论模型或者非概率模型,对应由条件概率分布\(P(Y|X)\)或者决策函数\(Y=f(X)\)来表示。
根据输入输出变量的不同,对不同的预测任务给予不同的名称:
- 回归问题:输入变量和输出变量均为连续变量
- 分类问题:输出变量为有限个离散变量
- 标注问题:输入变量和输出变量均为变量序列
无监督学习(unsupervised learning)是指从无标注数据中学习预测模型的机器学习问题。无监督学习的本质是学习数据中的统计规律或者潜在结构。同样,在无监督学习中,也存在输入空间、输出空间、特征空间的概念。
强化学习(reinforcement learning)是指智能系统在与环境的连续互动中学习最优行为策略的机器学习问题。假设智能系统与环境的互动基于马尔可夫决策过程,智能系统能观测到的是与环境互动得到的数据序列。强化学习的本质是学习最优的序贯决策。
半监督学习(semi-supervised learning)是指利用标注数据和未标注数据学习预测模型的机器学习问题,通常有少量标注数据、大量未标注数据。半监督学习旨在利用未标注数据中的信息来辅助标注数据,进行监督学习,以较低的成本达到较好的效果。
主动学习(active learning)是指机器不断主动给出实例让教师进行标注,然后利用标注的数据学习预测模型的机器学习问题。通常的监督学习使用给定的标注数据,可以看作是“被动学习”。主动学习的目标是找出对学习最有帮助的实例让教师进行标注,以较小的标注代价达到较好的学习效果。
其中,半监督学习和主动学习更加接近监督学习。
按模型分类
按照模型的种类进行分类,可以有概率模型与非概率模型,线性模型与非线性模型,参数化模型和非参数化模型。
概率模型取条件概率分布形式\(P(y|x)\),非概率模型取函数形式\(y=f(x)\)。这两者可以相互转化,具体来说,条件概率分布最大化后得到函数,函数归一化之后得到条件概率分布。因此,概率模型和非概率模型的区别不在于输入与输出之间的映射关系,而在于模型的内在结构。
尤其对于非概率模型来说,可以分为线性模型和非线性模型。如果函数\(y=f(x)\)是线性函数,则称模型是线性模型,否则是非线性模型。深度学习实际上是复杂神经网络的学习,也就是复杂的非线性模型的学习。通常情况下,深度学习帮助模型进行特征的抽取。
参数化模型假设模型参数的维度固定,模型可以由有限维参数完全刻画;非参数化模型假设模型参数的维度不固定或者说无穷大,随着训练数据量的增加而不断增大。
按算法分类
根据算法,机器学习可以分为在线学习与批量学习。
在线学习是指每次接受一个样本,进行预测,之后学习模型,并不断重复该操作。与之对应,批量学习是一次接受所有的数据,学习模型后进行预测。在线学习通常比批量学习更难,很难学到预测精确率更高的模型,因为每次模型更新中可利用的数据有限。
按技巧分类
机器学习方法也可以按照使用的技巧分类。
贝叶斯学习又称为贝叶斯推理,是统计学、机器学习中重要的方法。它的主要思想是:在概率模型的学习和推理中,利用贝叶斯定理,计算在给定条件下模型的条件概率,即后验概率,并应用这个原理进行模型的估计。贝叶斯估计与极大似然估计在思想上有很大的不同,代表着统计学中贝叶斯学派和频率学派对统计的不同认识。
核方法是使用核函数表示和学习非线性模型的一种机器学习方法。把线性模型扩展到非线性模型,直接的做法是显式地定义从输入空间(低维空间)到特征空间(高维空间)的映射,在特征空间中进行内积计算。核方法的技巧在于不显式地定义这个映射,而是直接定义核函数,即映射之后在特征空间的内积。这样可以简化计算,达到同样的效果。
假设\(x_1,x_2\)是输入空间的任意两个向量,内积为\(<x_1,x_2>\),从输入空间到特征空间的映射为\(\varphi\),则对应向量在特征空间中的映像为\(\varphi (x_1), \varphi (x_2)\),内积为\(<\varphi (x_1), \varphi (x_2)>\)。核方法完成的是直接在输入空间中定义核函数\(K(x_1,x_2)\),需要满足: \[ K(x_1,x_2) = <\varphi (x_1), \varphi(x_2) > \]
机器学习三要素
机器学习总的目的是考虑学习什么样的模型和如何学习模型。
概括来说,首先我们有的是给定的、有限的、用于学习的训练数据training data,我们假设这些数据是独立同分布的,这些数据能够由某个真实函数\(g\)得来,但是这个真实函数\(g\)我们并不能精确的知道,我们能做的是通过学习得到某种函数\(f\),使得这个函数\(f\)能够尽可能地与真实函数\(g\)相同。在学习之前,我们需要确定需要学习的函数\(f\)所处在的函数集合,称之为假设空间\(H,(hypothesis\ space)\),通俗地说假设空间就是函数\(f\)长什么样子,假设空间的确定意味着学习的范围确定。之后我们需要应用训练数据来进行模型学习,这里需要应用某个评价准则,从假设空间中选取一个最优的模型。最优的含义是它在已知的训练数据以及未知的测试数据下有最优的表现。具体最优模型的选择过程则由算法来实现。
上面便是整个机器学习的过程,从中可以抽取出三个非常重要的概念,也是机器学习的三要素:
- 模型:包含所有可能的模型的假设空间(从哪里选择模型)
- 策略:模型选择的准则(按照什么标准选择模型)
- 算法:求解最优模型的算法(实际经过什么样的过程能够选到模型)
机器学习的过程也可以用下图来表示,可以说构建一种机器学习方法就是确定具体的机器学习三要素。
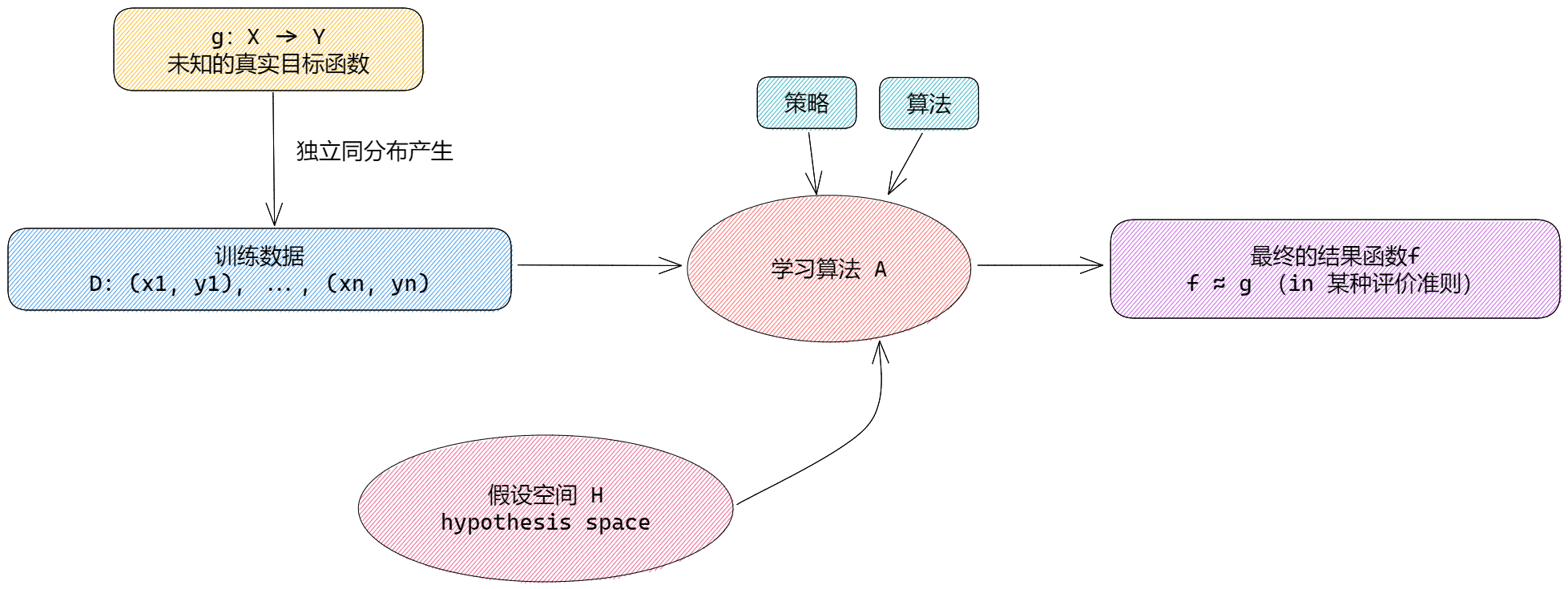
机器学习首要考虑的问题就是学习什么样的模型。在监督学习中,模型就是所要学习的条件概率分布函数或者决策函数。假设空间是函数的集合,这些函数通常是由一个参数向量决定的函数族。
有了模型的假设空间之后,机器学习接着需要考虑按照什么样的准则学习或者选择模型。策略(误差衡量的方式)的不同会影响我们最终从假设空间中如何选择一个作为最好的结果。首先引入损失函数和风险函数的概念。损失函数度量模型一次预测的好坏,风险函数度量模型在平均意义下预测的好坏。
这里我们假设从假设空间\(H\)中选取的模型为\(f\),损失函数度量模型一次预测的好坏,它是\(f(X)\)和\(Y\)的非负实值函数,记作\(L(Y,f(X))\)。
常用的损失函数由如下几种:
- 0-1损失函数:
\[ L(Y,f(X)) = \begin{cases} 1,\quad Y \neq f(X)\\ 0, \quad Y =f(X) \end{cases} \]
- 平方损失函数:
\[ L(Y,f(X)) = (Y-f(X))^2 \]
- 绝对损失函数:
\[ L(Y,f(X)) = |Y-f(X)| \]
- 对数损失函数(对数似然损失函数):
\[ L(Y,f(X)) = -logP(Y|X) \]
风险函数度量平均意义下模型预测的好坏,或者称为期望风险,它是模型\(f(X)\)关于真实的联合概率分布\(P(X,Y)\)的期望,记作\(R_{exp}\): \[ \begin{aligned} R_{exp}(f) &= E_P[L(Y,f(X))] \\ &=\int _{X \times Y} L(y,f(x))P(x, y)dxdy \end{aligned} \] 另一个概念是经验风险或者经验损失,它是模型\(f(X)\)关于训练数据集的平均损失,记作\(R_{emp}\): \[ R_{emp}(f) = \frac{1}{N}\sum_{i=1}^{N}L(y_i,f(x_i)) \]
在相关笔记的描述中,还会出现\(E_{in}\)和\(E_{out}\)的表述,它们分别代表经验损失以及期望风险。
学习的目标就是选择期望风险最小的模型。但是真实的联合概率分布\(P(X,Y)\)是未知的,就导致我们无法直接计算风险函数\(R_{exp}\)。实际上,如果我们知道真实的联合概率分布,那么也就可以直接求出条件概率分布函数,就无需学习了。期望分析\(R_{exp}(f)\)是模型关于真实联合分布的期望损失,经验风险\(R_{emp}(f)\)是模型关于训练集的平均损失。根据大数定律,当样本容量N趋于无穷,经验风险趋于期望风险。因此一个很自然的想法是用经验风险估计期望风险。但是实际上训练样本有限,这种方式并不是很理想,还需要对经验风险进行一定的矫正。这就关系到监督学习的两个基本策略:经验风险最小化和结构风险最小化。
经验风险最小化(empirical risk minimization,ERM)直接认为经验风险最小的模型就是最优的模型,它需要求解的最优化问题如下: \[ \min_{f\in D}R_{emp}(f) = \min_{f\in D}\frac{1}{N}\sum_{i=1}^{N}L(y_i,f(x_i)) \] 当样本容量足够大,经验风险最小化能够保证有很好的学习效果。但是当样本容量很小的时候,经验风险最小化的效果未必很好,会产生过拟合的现象。
结构风险最小化(structural risk minimization,SRM)是为了防止过拟合而提出来的策略,它等价于正则化。结构风险在经验风险上增加表示模型复杂度的正则化项或者惩罚项。结构风险记作\(R_{srm}\): \[ R_{srm}(f) =\frac{1}{N}\sum_{i=1}^{N}L(y_i,f(x_i)) + \lambda J(f) \] 其中,\(J(f)\)为模型的复杂度,模型越复杂,该项的值越大,表示对模型复杂度的惩罚。\(\lambda\)则是一个系数,用来权衡经验风险和模型复杂度。结构风险最小化的策略对应下面的最优化问题,结构风险小的模型往往对训练数据以及未知的测试数据都有较好的预测: \[ \min_{f\in D} R_{srm}(f) =\min_{f\in D} \frac{1}{N}\sum_{i=1}^{N}L(y_i,f(x_i)) + \lambda J(f) \] 算法指的是学习模型的具体计算方法。如果最优化问题有显式的解析解,这个最优化问题就比较简单。但更多的情况是解析解并不存在,此时则需要使用数值计算的方法来进行求解。如果保证找到全局最优解,并使得求解的过程非常高效,就是算法需要考虑的问题。
模型评估与模型选择
通常不同的学习方法会给出不同的模型,我们需要评估不同模型的好坏。我们使用损失函数来评估不同模型的好坏,主要看基于损失函数的模型的训练误差和测试误差。这里的损失函数与前面机器学习策略中提到的损失函数指的是相同的东西,只不过起到的作用不同。值得注意的是,机器学习策略具体采用的损失函数未必是评估时使用的损失函数,不过让两者保持一致通常是比较理想的。
如果一味追求提高模型对训练数据的预测能力,所选模型的复杂度往往会比真实模型更高,这种现象被称为过拟合。过拟合指的是学习时所选择的模型所包含的参数过多,导致模型对已知数据预测得很好,但是对未知数据预测得很差。模型选择时,应该避免过拟合并提高模型的泛化能力。
下图描述了训练误差和测试误差与模型复杂度之间的关系。当模型复杂度增大,训练误差会逐渐减小并趋近于0;而测试误差会先减小,达到最大值后又增大。
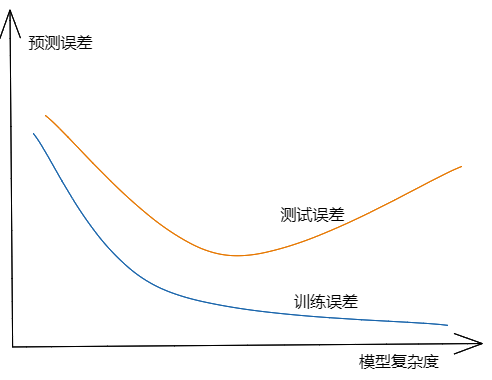
正则化与交叉验证
正则化和交叉验证都是模型选择的方式。
正则化
正则化(regularization)是结构风险最小化策略的实现,它在经验风险上增加一个正则化项或者是惩罚项。正则化项一般是模型复杂度的单调递增函数,模型越复杂,正则化值越大。在选择模型时,选择正则化后结构风险最小的模型。
举例来说,正则化项可以是模型参数向量的范数。例如在回归问题中,损失函数是平方损失,正则化项则是参数向量的L2范数或者L1范数,\(\lambda\)则是一个事先给定的,用来调节惩罚项限制程度的参数: \[ L(w) = \frac{1}{N} \sum_{i=1}^{N}(f(x_i;w) - y_i)^2 + \frac{\lambda}{2}||w||^2 \] 其中\(||w||\)表示参数向量\(w\)的L2范数。 \[ L(w) = \frac{1}{N} \sum_{i=1}^{N}(f(x_i;w) - y_i)^2 + \lambda||w||_1 \] 其中\(||w||_1\)表示参数向量\(w\)的L1范数。
向量范数:
- L0范数:向量中非零元素的个数
- L1范数:向量各元素绝对值之和
\[ ||w||_1 = \sum_{i=1}^{n}|w_i| \]
- L2范数:向量的长度
\[ ||w||_2 = ||w|| = \sqrt{\sum_{i=1}^{n}w_i^2} \]
交叉验证
交叉验证(cross validation)则是另一种常用的模型选择方法。
在给定样本数据充足的情况下,进行模型选择的方法是将数据集随机切分成三个部分,分别是训练集、验证集和测试集。训练集用来训练模型,验证集用于对模型的选择,而测试集用于最终对学习方法的评估。在从不同的假设空间\(H\),学习到的不同复杂度的模型中,选择对验证集有最小预测误差的模型。如果数据量充足,这种方式是有效的,但是在许多实际情况中,我们的数据并不充足。此时可以采用交叉验证方法,它的基本思想是重复地利用数据,将给定的数据进行切分,切分后的数据集组合为训练集和测试机,在此基础上反复训练、测试和模型选择。
1.简单交叉验证
首先随机将数据分为两部分训练集和测试集(例如7:3),用训练集在各种条件下训练模型,从而得到不同模型。在测试集上评估各个模型的误差,选择测试误差最小的模型。
通过这种方式选择出来的模型告诉我们这个模型(模型+策略+算法)面对这个问题能够得到好的效果,但是这个模型有没有达到目前的极限呢?由于我们使用的训练集是给定数据的一部分,而在大部分情况下,训练数据越多,我们能够得到越好的效果。因此在实际操作的时候,一般会将选择出来的模型,在原本给定的所有数据上重新进行训练,以期能够得到更好的结果。
2.K折交叉验证
首先随机将数据分为K个互不相交,大小相同的子集。依次选择其中K-1个子集的数据训练模型,选择剩下一个子集的数据测试模型。这个过程重复K次,可以得到K个测试结果,以平均测试误差作为该模型的测试误差,选择对应误差最小的模型。
3.留一交叉验证
K折交叉验证中K = N的特殊情况,N为样本总数。这种方法往往在数据缺乏的情况下使用。它的时间复杂度相对较高,因为对于一个模型来说,需要在相差不大的数据上重复训练N次。
监督学习应用
监督学习的应用主要在三个方面:分类问题、标注问题和回归问题。
分类问题中,输出变量取值为有限个离散值。评价分类器性能的指标一般是分类精确率(accuracy),它的定义是对于给定的测试数据集,正确分类的样本占总样本数的比例。
注意精确率accuracy和准确率precision的定义差别。
对于二分类问题,常用的评价指标是准确率(precision)和召回率(recall)。在二分类的预测结果中会出现下面四种情况:
- TP:正确地预测为正类,真实为正类
- FN:错误地预测为负类,真实为正类
- FP:错误地预测为正类,真实为负类
- TN:正确地预测为负类,真实为负类
上面,T/N 表示预测是否正确,P/N 表示预测的结果,而真实的结果需要结合T/N来判断。
在上面定义的四种情况下,准确率定义如下,它表示在所有预测为正类的结果中,预测正确的所占的比例: \[ P = \frac{TP}{TP+FP} \] 召回率定义如下,它表示在所有真实为正类的结果中,预测正确的所占的比例: \[ R = \frac{TP}{TP+FN} \] 此外还有一个评价指标是\(F_1\)值,它是准确率和召回率的调和平均值,准确率和召回率都高的时候,\(F_1\)值也会高: \[ \frac{2}{F_1} = \frac{1}{P} + \frac{1}{R} \\ F_1 = \frac{2TP}{2TP+FP+FN} \] 标注问题的输入是一个观测序列,输出是一个标记序列或者状态序列。自然语言处理中的词性标注就是一个典型的标注问题。评价标注模型的指标与评价分类模型的指标一样,常用的有标注精确率、准确率和召回率等。定义与分类模型相同。标注问题常用的机器学习方法有隐马尔可夫模型、条件随机场等。
回归问题的输出是连续的值。回归模型表示从输入变量到输出变量之间的映射,回归问题的学习等价于函数拟合。回归学习最常用的损失函数是平方损失函数,在这种情况下,回归问题可以由最小二乘法求解。
参考资源
本系列(机器学习基础)参考林轩田老师的《机器学习基石》和《机器学习技法》课程,相关参考资源如下,后续不再单独列出。