机器学习基础(4)-过拟合,正则化与Validation验证
过拟合
现象描述
在之前机器学习可行性的说明中,我们看到了一张经验损失\(E_{in}\),期望损失\(E_{out}\)以及VC Dimension的变化图,其中随着VC Dimension的增大,我们发现经验损失在逐渐降低,而期望损失先降低后增大。这也就是说,随着模型逐渐变得复杂,虽然我们能够在训练集上做的很好,但是在训练集之外的数据表现还是很糟糕,也就是泛化能力差。这种情形我们称之为过拟合。相对的,当模型比较简单的时候,经验损失和期望损失都较高,这种情形称之为欠拟合。一般来说,欠拟合只需要增加模型复杂度或者增加训练数据,解决起来相对简单。我们这里仅考虑过拟合的现象。
通常来说,影响过拟合的因素有三个:
- 模型复杂度过高,VC Dimension过大
- 数据中存在较多的噪声noise
- 训练样本的数量N不够
VC Dimension对过拟合现象的描述已经可以通过图像表示,接下来我们关注噪声和样本数量对过拟合的影响。首先考虑样本数量,假设我们有上帝视角,直到真实的映射函数是一个10次多项式的形式,那么我们自然会想到利用一个也是10次多项式的假设空间。但是这也会存在一个问题,我们可以通过Learning Curve图像来观察。Learning Curve图像是误差随着样本数量变化的曲线,其中左图表示我们选择的假设空间\(H_{2}\)最多能够表示2次多项式,而右图表示假设空间\(H_{10}\)最多能够表示10次多项式。
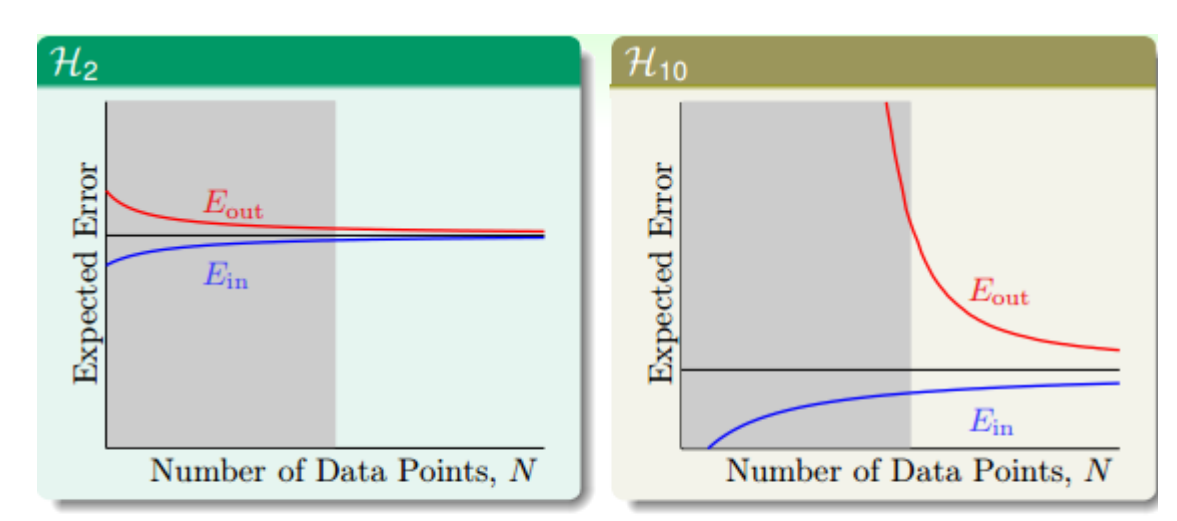
直觉上来说,我们认为既然真实的目标函数是一个10次多项式,那么我们也用10次多项式的假设空间进行学习,应该能够得到一个很好的结果。但是实际上,效果与训练集数据的数目\(N\)是由很大关系的。对比\(H_2\)和\(H_{10}\),我们可以发现的确\(H_{10}\)能够最终做到很好,也就是\(E_{in}\)和\(E_{out}\)都能做到不错,但是这是建立在足够\(N\)的基础上的,但是如果\(N\)不足以支撑\(H_{10}\)做到较低的\(E_{out}\),那么它的效果可能还不如较简单的模型\(H_2\)。总结来说,在这种情况下,数据量不足导致较复杂模型的表现不如简单模型,复杂模型的\(E_{in}\)较低,但是\(E_{out}\)比较高,也就是过拟合的表现。
接下来我们考虑噪声对过拟合的影响。通常,我们可以认为噪声服从正态分布。假如一个模型很强大,它在训练集上将\(E_{in}\)做的很好,但是这个训练集中是存在较多噪声的,这也就是说模型将噪声也学进结果里面了,在没有规律的地方硬学出了规律,自然会导致泛化能力不足。而实际上还有另一种情况,就是真实的目标函数就是很复杂,而我们使用的假设空间不足以描述这么复杂的函数。这样,从真实函数中得到的训练集,尽管其中没有噪声,但是对于较弱的假设空间来说,它所带来的影响同噪声没有什么区别。不过这种噪声并不是随机产生的,而是与真实函数有关,因此我们将它称为deterministic noise,确定性误差。而之前那种真实的误差,则称为stochastic noise,随机误差。
总结来说,有三个方面的因素会影响过拟合。分别是过高的模型复杂度,较多的噪声(包括确定性误差以及随机误差)以及不足的训练集样本数。
解决方法
过拟合的影响因素主要有三个,而解决过拟合的方法自然也能够从这三个因素出发。
对于过高的模型复杂度,我们通常会选择从简单的模型出发进行训练,然后逐步提高模型的复杂度。对于一个机器学习问题来说,如果我们能够用简单且效果不错的模型解决,那么我们就不要去选择更加复杂的模型,这也符合哲学中的“奥卡姆剃刀原则”。另一种解决方式正则化,它用来控制模型的复杂度,接下来会进行详细说明。
对于较多的噪声,我们可以在训练之前进行数据清洗,尽量减少噪声在训练集中的比例。
对于不足的训练集样本数,那我们就增加训练集样本数就好了。当然更多的情况是我们没办法直接得到更多的训练集样本,此时可以考虑从已有的训练集出发,通过合理的方式得到更多的数据。这里需要注意的是,新样本的产生一定要合理,否则会破坏机器学习的假设,即训练集来自于真实存在的目标函数的假设。
正则化
概念引入
正则化(Regularization)是一种控制模型复杂度的方法,通常用来解决过拟合问题。
仍然考虑上面的场景,我们分别用10阶多项式假设空间\(H_{10}\)以及2阶多项式假设空间\(H_{2}\)进行模型训练,在数据量较少的情况下,2阶多项式表现更好。但是我们并不想放弃\(H_{10}\)假设空间,因为2阶多项式假设空间表征能力有限。所以我们现在的目标就是怎么样增加一定的限制,在保留\(H_{10}\)表征能力的同时,控制\(H_{10}\)复杂度的同时,让\(H_{10}\)的表现尽可能向\(H_{2}\)靠近。
对于一个模型来说,我们最终需要得到一个参数向量\(w\)。一个给定参数向量\(w\)对应到一个确切的模型。因此参数向量一定程度能够表征模型的复杂度。\(H_{10}\)的假设空间可以对应11维的向量\(w=[w_0,w_1,...,w_{10}]^T\),而\(H_2\)的假设空间可以对应3维的向量\(w=[w_0,w_1,w_2]^T\),并且始终有\(H_2 \subseteq H_{10}\)的关系存在,我们可以限制\(w_3=w_4=...=w_{10}=0\),此时则有\(H_2=H_{10}\)。
但是这个限制实际上较为严格,我们限制\(H_{10}\)的高阶部分权重均为0,那既然如此不如直接使用\(H_2\)。因此我们可以适当放宽限制,例如让\(H_{10}\)的任意8个权重为0,即\(\sum_{i=0}^{10}I[(w_i \neq 0)] \le 3\),也就是限定参数向量中不为0的维度个数,而并不一定要限定高阶部分权重为0。不过这种条件会带来另外的问题,就是它不好优化。因此我们考虑一种容易求解的更加宽松的条件,即: \[ \sum_{i=0}^{10}w_i^2 = ||w||^2 \le C \] 这个限制条件的含义是权重的平方和大小不超过一个给定的常数C,这个常数C用来限制参数向量。可以想见的是,C的值越大,限定范围越大,即限定条件越宽松,反之则越严格。因此,对于我们需要解决的机器学习问题来说,最终就会对应到一个带限制条件的最优化问题,优化目标如下,其中的限制是上面的不等式。 \[ \min_{w} E_{in} = \frac{1}{N} \sum_{i=1}^{N}L(w,x_i,y_i) \\ \text{并且需要满足:} \sum_{i=0}^{10}w_i^2 = ||w||^2 \le C \] 限制条件的几何含义是,权重向量\(w\)被限制在一个半径为\(\sqrt{C}\)球内,球外的\(w\)都不在我们的考虑范围内。在这个限制条件下,我们进行梯度下降,每一步实际上都是更加靠近无限制的目标\(w_{no-limit}\),只不过在限制条件下,我们的\(w\)只能在球内移动,也就是移动方向必须垂直当前\(w\)所在位置的法向量。因此最终的结果一定在这个球的表面上,即满足\(||w||^2 = C\)。(如果\(w_{no-limit}\)直接在球的内部,那就可以直接梯度下降得到答案,相当于没有限制,这里不考虑这种情况)
所以优化问题可以继续转化为带等式约束的最优化问题: \[ \text{优化目标}:\min_{w} E_{in}(w) = \frac{1}{N} \sum_{i=1}^{N}L(w,x_i,y_i) \\ \text{约束条件}: ||w||^2 - C = 0 \] 带等式约束的最优化问题可以使用拉格朗日乘数法来解决,引入辅助变量\(\lambda\)以及辅助函数\(L'(w,\lambda)\): \[ L'(w,\lambda) = E_{in}(w) + \lambda (w^Tw-C) \]
则极值点需要满足: \[ \bigtriangledown _{w} E_{in}(w) + 2\lambda w = 0 \] 类比我们无限制的最优化问题,我们需要最优化的目标是\(\min_w E_{in}(w)\),需要满足的条件是\(\bigtriangledown _w E_{in}(w)= 0\)。而对于带限制的最优化问题,我们需要满足的条件是\(\bigtriangledown _{w} E_{in}(w) + 2\lambda w = 0\),可以类比得到最优化的目标是\(\min_w E_{in}(w) + \lambda w^Tw = E_{in}(w) + \lambda ||w||^2\)。因此我们最终将问题转化为如下的描述,对应给定的假设空间\(H\),需要找到一个参数向量\(w\),最小化下面的目标: \[ \min_w E_{in}(w) + \lambda ||w||^2 \] 其中\(\lambda\)是预先给定的常数。实际上这就是正则化做的事情。与之前不带正则化的机器学习相比,只是在优化目标中增加了一个正则项。
与VC Theory的关系
考虑正则化与VC Theory之间的关系。我们可以将增加的正则化项记作\(\Omega(w)\),它用来表示给定的单个模型的复杂度。经过正则化之后的损失可以记作\(E_{reg}(w)\),则有: \[ E_{reg}(w) = E_{in}(w) + \Omega(w) \] 而VC不等式表示如下,其中\(\Omega(H)\)表示整个假设空间的复杂度。 \[ E_{out}(w) \le E_{in}(w) + \Omega(H) \] 单个模型的复杂度包含于整个假设空间的复杂度中,因此可以看出\(E_{reg}\)相比于\(E_{in}\)来说,更加接近于\(E_{out}\),因此能够更好地代表它,从而能够降低过拟合的风险。
正则化项
上面的正则化我们是针对多项式假设空间的,而事实上,正则化的思想可以应用在所有的机器学习算法中,用来防止过拟合。我们在基础的经验损失上增加正则化项,表示对模型复杂度的惩罚。并且引入\(\lambda\)来表示惩罚的力度,\(\lambda\)越大,表示惩罚越大,对模型的限制越高。一般来说,\(\lambda\)取较小的值就能够达到良好的拟合效果,过大过小都会有问题。不过究竟取什么值,还需要根据具体训练数据和模型进行分析和调试。
上面推导出的正则化项是利用了参数向量的L2范数,常用的正则化项还有参数向量的L1范数等。
那么在实际的使用中,正则化项\(\Omega(w)\)该选择如何的形式呢。常见的选择方式有三种。第一种是目标导向的,即在任务中有很直接的方式告诉我们模型复杂度该如何衡量。第二种是选择常用的正则化项,例如L2范数、L1范数等。第三种是选择一个便于优化的正则化项。
Validation验证
概念引入
在机器学习中,我们会遇到很多的选择问题。首先我们需要选择使用什么模型,假设空间\(H\)是什么,学习算法\(A\)是什么,学习率\(\eta\)也需要确定,正则化项\(\Omega(w)\)需要确定,对应的\(\lambda\)也需要确定。我们需要做多方面的选择,不同的选择搭配,有不同的机器学习效果。而我们希望的就是能够找到一个最合适的选择搭配,得到一个优秀的结果模型,产生最佳的效果。
重新描述选择问题,就是说我们现在一共有\(M\)种候选模型(广义上的模型,表示上面各种选择的一种搭配),然后目标是从中选择一个模型作为最终的结果模型。我们很自然的就想到以目标为导向,哪个模型在测试集上表现最好,我们就选择哪个模型。但是很不幸的是,测试集是我们拿不到的数据。那我们就考虑从拿得到的数据即训练集中进行评估。但是如果用训练集进行训练,然后又用训练集进行评估,会存在偷窥数据作弊的嫌疑。在使用数据的过程中,我们应该要非常的谨慎,防止偷看数据。
如果我们综合上面两种思路,就可以得到验证Validation的思想。简单来说就是将训练集进行划分,划分为新训练集和验证集。模型在新训练集上完成训练后,在验证集上进行评估,评估结果就作为模型效果。最后我们就可以选择一个模型效果最好的作为结果模型。
交叉验证
交叉验证的思想在之前的笔记中已经有记载,下面的内容与之前相同。
在给定样本数据充足的情况下,进行模型选择的方法是将数据集随机切分成三个部分,分别是训练集、验证集和测试集。训练集用来训练模型,验证集用于对模型的选择,而测试集用于最终对学习方法的评估。在从不同的假设空间\(H\),学习到的不同复杂度的模型中,选择对验证集有最小预测误差的模型。如果数据量充足,这种方式是有效的,但是在许多实际情况中,我们的数据并不充足。此时可以采用交叉验证方法,它的基本思想是重复地利用数据,将给定的数据进行切分,切分后的数据集组合为训练集和测试机,在此基础上反复训练、测试和模型选择。
1.简单交叉验证
首先随机将数据分为两部分训练集和测试集(例如7:3),用训练集在各种条件下训练模型,从而得到不同模型。在测试集上评估各个模型的误差,选择测试误差最小的模型。
通过这种方式选择出来的模型告诉我们这个模型(模型+策略+算法)面对这个问题能够得到好的效果,但是这个模型有没有达到目前的极限呢?由于我们使用的训练集是给定数据的一部分,而在大部分情况下,训练数据越多,我们能够得到越好的效果。因此在实际操作的时候,一般会将选择出来的模型,在原本给定的所有数据上重新进行训练,以期能够得到更好的结果。
2.K折交叉验证
首先随机将数据分为K个互不相交,大小相同的子集。依次选择其中K-1个子集的数据训练模型,选择剩下一个子集的数据测试模型。这个过程重复K次,可以得到K个测试结果,以平均测试误差作为该模型的测试误差,选择对应误差最小的模型。
3.留一交叉验证
K折交叉验证中K = N的特殊情况,N为样本总数。这种方法往往在数据缺乏的情况下使用。它的时间复杂度相对较高,因为对于一个模型来说,需要在相差不大的数据上重复训练N次。