机器学习基础(6)-线性回归与Logistic回归

线性回归

模型描述

在机器学习中，一个最常见的模型就是线性回归模型。这个模型的输入是一个多维的向量\(x\in X\)，而输出是一个实数\(y\in R\)，整个模型可以描述如下： \[ y = h(x) = w^Tx + b = \hat{w}^T \hat{x} \] 其中的\(w\)为参数向量，模型可以看作是参数向量与输入向量的内积结果。这里可以将偏置项\(b\)统一到参数向量中，将参数向量扩充为\(\hat{w}\)。为了简单起见，如果没有特殊说明，后续的参数向量\(w\)实际上指的都是扩充后的\(\hat{w}\)。从几何角度来看，如果输入空间是一维空间，则线性回归的目标是找到一条直线，使得样本集中的点更加接近它。如果输入空间是高维空间，则目标是找到一个（超）平面。

损失函数通常使用的是平方误差，即： \[ L(w,x_i,y_i) = (y_i - y)^2 = (y_i-w^Tx_i)^2 \] 在使用平方误差的基础上，这里的线性回归问题与统计学中的线性回归问题是相同的，我们可以通过最小二乘法来解决该问题。

最小二乘法

假设我们的训练集的容量为N，即\(D = \{x_1,x_2,...,x_N\}\)，同时每个\(x_i\)都是一个\(d\)维向量。考虑我们的优化目标，让模型在训练集上达到最小的平方误差，即： \[ \min_{w}E_{in}(w) = \min_{w} \frac{1}{N}\sum_{i=1}^{N}(x_i^Tw-y_i)^2 \] 这里的参数向量\(w\)是扩充后的向量，\(x_i\)也增加了常数维度，此时是一个\(d+1\)维向量。与上面的损失函数表示方式不同，这里交换了\(x\)与\(w\)的位置，这是为了后续的矩阵化处理，并不会影响结果的正确性。

对于上面的式子，我们可以使用矩阵来简化\(E_{in}\)的表达方式： \[ \begin{aligned} E_{in}(w) &= \frac{1}{N}\sum_{i=1}^{N}(x_i^Tw-y_i)^2\\ &= \frac{1}{N} || \begin{bmatrix} x_1^Tw-y_1\\ x_2^Tw-y_2\\ ...\\ x_N^Tw-y_N \end{bmatrix} ||^2 \\ &=\frac{1}{N}|| \begin{bmatrix} x_1^T\\ x_2^T\\ ...\\ x_N^T \end{bmatrix} w- \begin{bmatrix} y_1\\ y_2\\ ...\\ y_N \end{bmatrix} ||^2\\ &=\frac{1}{N}||Xw-Y||^2 \end{aligned} \] 于是有\(E_{in}(w)=\frac{1}{N}||Xw-Y||^2\)。其中\(X\)是一个\(N\times(d+1)\)的矩阵，每一行是训练集中扩充后的输入向量\(x_i\)；\(w\)是一个\((d+1)\times1\)的矩阵，每一行是一个对应的参数；\(Y\)是一个\(N\times1\)的矩阵，每一行是训练集中对应的结果\(y_i\)。

我们想要找到一个\(w\)使得\(E_{in}(w)\)达到最小值，也就是找到在函数梯度为0的地方对应的\(w\)。即\(\bigtriangledown E_{in}(w) = 0\)。下面我们可以计算\(E_{in}(w)\)的梯度： \[ \begin{aligned} E_{in}(w) &= \frac{1}{N}||Xw-Y||^2 = \frac{1}{N}(w^TX^TXw-2w^TX^TY+Y^TY)\\ \bigtriangledown E_{in}(w) &= \frac{1}{N}(2X^TXw-2X^TY) = \frac{2}{N}(X^TXw-X^TY) \end{aligned} \] 于是如果想要梯度为0，也就是： \[ X^TXw=X^TY \] 如果\(X^TX\)可逆，我们可以得到对应的\(w=(X^TX)^{-1}X^TY\)。实际上，如果\(X^TX\)不可逆，数学上仍然可以找到一个解析解。也就是说，对于线性回归问题，在使用平方误差的前提下，我们可以直接计算出最优参数向量\(w\)的解析解。

我们可以从几何意义上来考虑最小二乘法的含义。

首先我们的原始目的在于最小化\(Xw-Y\)。如果我们能够找到一个\(w\)，能够满足\(Xw-Y=0\)，那么也就是找到了一条直线（一个超平面）能够完全拟合给定的数据点。但是通常给定的数据不会刚好能够完全拟合，因此需要另寻途径。不过我们仍然可以考虑上面这种想法背后的含义。如果\(Xw-Y=0\)即\(Xw=Y\)，它表示如果将\(Y\)看作是一个\(N\)维的向量，我们能够使用\(D=\{x_1,x_2,...,x_N\}\)的线性组合来表示\(Y\)向量，也就是\(Y\)恰好落在\(D=\{x_1,x_2,...,x_N\}\)所张成的空间中。当然这种情况出现的可能性很小，对应给定的数据通常不会刚好能够完全拟合。

在最小二乘法中，考虑的是等式\(X^TXw=X^TY\)，相当于在\(Xw=Y\)的两端同时施加一个线性空间变换，线性变换对应的矩阵维\(X^T\)，它是一个\((d+1)\times N\)的矩阵，表示从\(N\)维空间中的一个超平面变换到\(d+1\)维空间，此时再考虑变换后的\(Y\)。这一过程的含义是，如果在\(N\)维空间中，\(Y\)不能落在\(D=\{x_1,x_2,...,x_N\}\)张成的空间，那就考虑\(Y\)在该空间上的投影\(Y'\)。投影\(Y'\)与向量\(Y\)的距离在一定程度上也就能度量整体的损失。

Logistic回归

模型描述

考虑这样一个场景，我们仍然考虑一个二分类问题，但是对于给定的输入，我们要求的输出并不是它是A类还是不是A类，而是希望输出它是A类的概率。具体来说，对于输入\(x\)，我们希望输出的\(y\in[0,1]\)，可以看成被分到A类的概率，即\(y=P(f(x)=A|x)\)。

模型的构建可以参考线性回归模型。在线性回归模型中，对于输入\(x\)，我们可以得到一个在实数域上的输出\(y\)，如果能够在此基础上，将输出\(y\)映射到\([0,1]\)的范围，我们就可以得到符合上面场景的模型。实际上，Logistic回归就是使用这样的思想，它使用的函数为sigmoid函数（又称Logistic 函数），它有如下的定义以及图像：

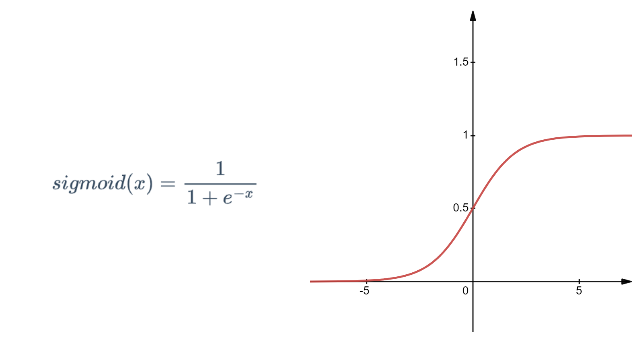
于是我们可以重新描述Logistic回归模型。我们的输入为一个多维向量\(x\in X\)，输出为\(y\in[0,1]\)，参数向量为\(w\)，则有如下的描述： \[ y =h(x) = sigmoid(w^Tx+b) = \frac{1}{1+\exp(\hat{w}\hat{x})} \] 与线性回归一样，这里同样可以进行输入向量\(x\)以及参数向量\(w\)的扩充，以增加上标的符号表示扩充后的向量。注意这里提供的训练集为\(D=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}\)，且其中\(y_i \in\{+1,-1\}\)。

损失函数

Logistic回归的输出是一个在\([0,1]\)范围内的实数，我们说这个实数\(y\)可以看作是将当前输入\(x_i\)分为+1的概率。考虑极大似然的思想，对于我们最终的模型\(h(x)\)来说，训练集出现的可能性\(P_{target}\)是最大的。考虑样本点\((x_i,y_i)\)，这个样本点出现的可能性的计算分为两个部分，第一部分是\(x_i\)出现的概率，记为\(P(x_i)\)，第二部分是\(x_i\)对应输出为\(y_i\)的概率，记为\(P(y_i|x_i)\)。考虑我们模型输出\(h(x)\)的含义，有如下的表达式成立： \[ P(y|x) = \begin{cases} h(x) ,\quad y = +1\\ 1-h(x), \quad y = -1 \end{cases} \] 所以样本点出现的可能性为： \[ P((x,y)) = \begin{cases} P(x)h(x) ,\quad y = +1\\ P(x)(1-h(x)), \quad y = -1 \end{cases} \] 而由于我们的模型最外层是sigmoid函数，使得模型具有性质\(1-h(x) = h(-x)\)，因此上面样本点出现的可能性可以转化为下面的表示： \[ \begin{aligned} P((x,y)) &= \begin{cases} P(x)h(x)=P(x)h(1\times x) ,\quad y = +1\\ P(x)(1-h(x))=P(x)h(-x)=P(x)h(-1\times x), \quad y = -1 \end{cases} \\ &=P(x)h(yx) \end{aligned} \] 因此模型的优化目标是最大化\(P_{target}\)，且有： \[ P_{target} =\prod_{i=1}^{N}P((x_i,y_i)) = \prod_{i=1}^{N}P(x)h(yx) \] 而通常情况下，我们希望处理的更多是连加而非连乘的形式，因此我们可以对上面的\(P_{target}\)进行取对数的操作来将连加转化为连乘，并引入平均数操作\(1/N\)。同时增加负号，将最大化变成最小化，由此模型的优化目标就转化成了下面的形式： \[ \min_{w} \frac{1}{N} \sum_{i=1}^{N} -\log(h(y_ix_i)) \] 同时将\(h(x)\)的表达式进行带入，那么就会转化为下面的形式： \[ \min_{w} \frac{1}{N} \sum_{i=1}^{N} \log(1 + \exp{(-y_iw^Tx_i)}) \] 实际上，后面的log项对应的是一个损失函数，叫做交叉熵（Cross Entropy）损失函数，即： \[ \text{cross entropy}(w,x,y) = log(1+\exp(-ywx)) \] 其中log的底数并没有强制的要求，不同的底数最终仅相差一个系数。

优化算法

有了上面的优化目标，我们就可以进行算法的描述。同样可以使用梯度下降法来进行。其中的关键在于优化目标函数的梯度计算。这里为了计算方便，取自然对数。 \[ \begin{aligned} E_{in}(w) &= \frac{1}{N} \sum_{i=1}^{N} \ln(1 + \exp{(-y_iw^Tx_i)})\\ 记&y_iw^Tx_i = A\\ \bigtriangledown E_{in}(w) &= \frac{1}{N} \sum_{i=1}^{N} \frac{e^{-A}}{1+e^{-A}}(-A)'\\ &= \frac{1}{N} \sum_{i=1}^{N} sigmoid(-y_iw^Tx_i)(-y_ix_i) \end{aligned} \] 于是可以得到优化过程如下：

1.首先初始化\(w_0\)

2.计算梯度\(\bigtriangledown E_{in}(w)\)，方式如上面的公式

3.迭代更新参数向量\(w\) \[ w \leftarrow w - \eta \bigtriangledown E_{in}(w) \]

通常我们可以使用线性回归在训练集\(D\)上直接计算出对应的解析解\(w_{线性回归}\)，并以此作为Logistic回归的初始化\(w_0\)。

解决线性分类问题

重新考虑原始的线性分类问题，在原始的线性分类中，对模型的评估标准是分类错误点的个数。但是这个问题的求解是NP-Hard问题。我们已经学习了线性回归以及Logistic回归，那么能否使用线性回归或者Logistic回归来解决线性分类问题呢。一个很直觉的想法是利用线性回归求得一个分数之后，与某个阈值threshold进行比较，如果大于阈值则认为是+1类，否则认为是-1类。而我们在介绍Logistic回归的时候，也是用二分类问题进行引入的。利用Logistic回归求得输入对应是+1类的概率，如果大于0.5则认为是+1类，否则认为是-1类。当然这是我们直觉的想法，不过实际上也是能够有效果的。

那么为什么线性回归和Logistic回归能够用在线性分类上呢。考虑三种方式的损失函数，线性分类对应的损失函数为0/1损失，线性回归对应的损失函数为平方损失，而Logistic对应的损失函数为交叉熵损失（这里底数取2）。令\(w^Tx=s\)（这个计算像是通过输入向量以及参数向量计算出某个分数score）：

对于线性分类来说，有： \[ \begin{aligned} h(x) &= sign(s)\\ err_{0/1}(s,y) &= I[sign(s) \neq y ]\\ &=I[sign(ys) \neq 1],I为指示函数\\ \end{aligned} \] 对于线性回归来说，有： \[ \begin{aligned} h(x) &= s\\ err_{sqr}(s,y) &= (s-y)^2 = (ys - 1)^2\\ \end{aligned} \] 对于Logistic回归来说，有： \[ \begin{aligned} h(x) &= sigmoid(s)\\ err_{ce}(s,y) &=ln(1+exp(-ys)) \end{aligned} \] 我们也可以作出它们的函数图像：

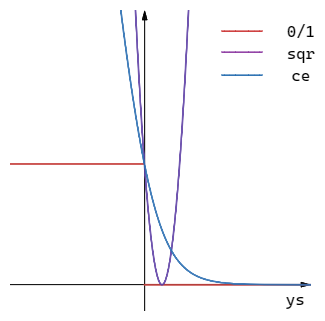
通过函数图像我们可以发现，始终有下面的不等式成立： \[ err_{0/1}\le err_{sqr}\\ err_{0/1}\le err_{ce} \] 重新考虑线性分类，我们说它能够机器学习，则需要VC Bound表达式的存在： \[ E_{out-线性分类} \le E_{in-线性分类} + \Omega_1(N,H,\delta) \] 又因为\(err_{0/1}\le err_{sqr}\)，所以有\(E_{in-线性分类} \le E_{in-线性回归}\)，所以有： \[ \begin{aligned} E_{out-线性分类} & \le E_{in-线性分类} + \Omega_1(N,H,\delta)\\ &\le E_{in-线性回归} + \Omega_2(N,H,\delta) \end{aligned} \] 这表示当我们使用线性回归来进行线性分类的时候，仍然可以解决问题，对应的\(E_{out}\)仍然存在上界，只不过这个上界变得更加宽松了。对于利用Logistic回归来解决线性分类问题也具有相同的解释。

多分类问题

上面的讨论都是二分类的情况，而多分类的情况可以由基本的二分类拓展得到。

扩展思想

One-Versus-All

对于多分类问题，我们可以将其想象为多个二分类问题。对于每个类别\(M\)，我们都可以将训练集划分为两部分，分别是属于类别\(M\)以及不属于这个类别。通过这样的数据，我们就可以训练一个关于类别\(M\)的二分类模型。对于每个类别我们都可以做这样的动作，如果一共有\(m\)个类别，那么我们就可以训练出\(m\)个不同的二分类模型。在最终输出的时候，这些二分类模型分别得到\(m\)个输出。如果二分类输出的是01是否这类的答案，可能会出现冲突的情况，此时我们可以使用Logistic回归来做二分类，得到概率的输出，最终选择概率最高的那个作为分类结果。

这种多分类的处理方式，我们称之为One-Versus-All（OVA）。它的优点是简单高效，缺点是会存在数据不平衡的方式。考虑存在\(m\)个类别，如果对于多分类来说数据分布是均匀的，那么我们在训练每个二分类模型的时候，正类数据占1份，负类数据占\(m-1\)份。数据不平衡会影响后续的分类效果。

One-Versus-One

OVA的方式由于数据不平衡，可能会影响分类效果。那我们考虑在训练二分类的时候，使用平衡的数据。具体来说，我们每次只取\(m\)个类中的2个类别的数据进行二分类模型的训练，例如AB两类。这样我们得到的模型能做到的事情就是将输入分成A类或者B类。对所有可能的2类取样进行二分类模型的训练，这样我们就可以得到\(\binom{m}{2}\)个二分类模型。对于给定的输入，我们分别调用这\(\binom{m}{2}\)个模型，对应得到\(\binom{m}{2}\)个输出，然后就可以通过投票的方式得到最终的输出。

这种多分类的处理方式，我们称之为One-Versus-One（OVO）。这种方式避免了出现数据不均衡，在训练二分类模型的时候也更加高效，因为训练数据减少了，每次仅需要进行两个类别的比较。但是这种方式需要训练的模型更多，时间复杂度和空间复杂度可能都比较高。

Softmax

对于多分类问题，我们也可以使用Softmax回归来解决。Softmax回归实际上就是Logistic回归的扩展，对于Logistic回归使用的sigmoid函数，我们可以将其看作是输出属于正类的概率，而Softmax函数定义如下： \[ \text{softmax}(x_i) = \frac{e^{x_i}}{\sum_{j=1}^n e^{x_j}} \] 在使用的过程中，我们可以通常输入一个向量，通过softmax得到输出向量，而输出向量的每个维度就可以看作是属于对应类别的概率。总结来说，softmax函数能够将未规范化的预测变换为全部非负并且总和为1的规范化概率预测，同时还可以保持函数可导的性质。softmax函数并不会改变预测的大小次序，而是确定每个预测的概率。