动手学深度学习(1)-预备知识
线性代数补充
向量点积 Dot Product
给定两个向量,它们之间的点积(dot product)是对应位置元素相乘并相加:
\[ \overrightarrow{a} \cdot \overrightarrow{b} = \sum_{i=1}^{n}a_ib_i = a_1b_1 + a_2b_2 + ...+a_nb_n \]
对应Pytorch中的操作:
1 | |
矩阵-向量积 Matrix-Vector Product
给定一个\(m \times n\)的矩阵\(A\)和一个\(n\)维向量\(x\),矩阵和向量的乘积有如下计算方式:
\[ Ax = \begin{bmatrix} a_1^T \\ a_2^T \\ ... \\ a_m^T \\ \end{bmatrix} x = \begin{bmatrix} a_1^T x \\ a_2^T x \\ ... \\ a_m^T x \\ \end{bmatrix} \]
矩阵向量积\(Ax\)是一个长度为\(m\)的列向量,其中第\(i\)个元素是向量点积\(a_i^Tx\)。
我们可以把一个矩阵\(A \in R^{m \times n}\)乘法看作一个从\(R^n\)到\(R^m\)向量的转换。 这些转换是非常有用的,例如可以用方阵的乘法来表示旋转。
矩阵乘法 Matrix-Matrix Multiplication
矩阵乘法即遵循前给行,后给列的计算方式,是矩阵-向量积的扩展。
注意,矩阵乘法不应该与Hadamard积混淆。Hadamard积(Hadamard product)表示的是矩阵按照对应位置元素进行相乘,数学符号为\(\odot\)。
1 | |
范数
简单地说,向量的范数是用来衡量一个向量有多大的。向量的范数并不局限于某一种计算方式,只要一个函数\(f\)能够将向量映射到标量,并且满足如下性质,那么我们就可以称这个函数是向量的范数。
\[ \begin{aligned} &1.[缩放] \ f(\alpha x) = |\alpha|f(x) \\ &2.[三角不等式]\ f(x+y) \le f(x) + f(y) \\ &3.[非负]\ f(x) \ge 0\\ &4.范数最小为0,当且仅当向量全由0组成 \end{aligned} \]
自然有很多函数都能够满足这些要求,在这些函数或者称为范数中,有一些常用的特殊范数,包括\(L_2\)范数、\(L_1\)范数、\(L_p\)范数等。
\[ \begin{aligned} &L_1范数: ||x||_1 = \sum_{i=1}^n |x_i|\\ &L_2范数: ||x||_2 = ||x|| = \sqrt{\sum_{i=1}^{n}x_i^2} \\ &L_p范数: ||x||_p = (\sum_{i=1}^n |x_i|^p)^{1-p}\\ \end{aligned} \]
在Pytorch中,这些范数可以通过下面的方式进行计算:
1 | |
类似于向量的\(L_2\)范数,矩阵\(X \in R^{m \times n}\)的Frobenius范数是矩阵元素平方和的平方根:
\[ ||X||_F = \sqrt{\sum_{i=1}^{m}\sum_{j=1}^{n}x_{ij}^{2}} \]
导数计算
函数推广
我们最熟悉的函数应该是\(y = f(x)\)的格式,这里的函数\(f(x)\)接受一个标量\(x\),输出另一个标量\(y\)。在线性代数里面我们引入了向量,矩阵等,于是函数也可以对应推广到标量、向量和矩阵版本。针对函数的类型和输入的类型,可以分为下面几类。
理解核心在于牢牢把握\(f\)的输出是一个标量,这样就可以清楚不同类型函数+不同类型输入的计算逻辑以及形状。
标量function
标量function称为实值标量函数,输出是一个标量,也是最基本的函数,使用符号\(f\)表示。
input可以是一个标量,例如:
\[ f(x) = ax+b \]
input可以是一个向量,例如:
\[ 设\mathbf{x} = [x_1, x_2, x_3]^T \\ f(\mathbf{x}) = ax_1 + bx_2 + cx_3 \]
input可以是一个矩阵,例如:
\[ \begin{aligned} &设 \mathbf{X}_{3 \times 2} = (x_{ij})_{i=1,j=1}^{3,2} \\ f(\mathbf{X}) &= a_1x_{11} + a_2x_{12} + a_3x_{13} + a_4x_{21} + a_5x_{22} + a_6x_{23} \end{aligned} \]
向量function
向量function称为实向量函数,输出是一个向量,使用符号\(\mathbf{f}\)表示,例如有:
\[ \mathbf{f}_{3\times 1} = \begin{bmatrix} f_1\\ f_2\\ f_3 \end{bmatrix} \]
input可以是一个标量,例如:
\[ \mathbf{f}_{3\times 1}(x) = \begin{bmatrix} f_1(x)\\ f_2(x)\\ f_3(x) \end{bmatrix} = \begin{bmatrix} a_1x+b_1\\ a_2x+b_2\\ a_3x+b_3 \end{bmatrix} \]
input可以是一个向量,例如:
\[ \begin{aligned} &设\mathbf{x} = [x_1, x_2, x_3]^T \\ \mathbf{f}_{3\times 1}(\mathbf{x})& = \begin{bmatrix} f_1(\mathbf{x})\\ f_2(\mathbf{x})\\ f_3(\mathbf{x}) \end{bmatrix} = \begin{bmatrix} a_1x_1+b_1x_2+c_1x_3\\ a_2x_1+b_2x_2+c_2x_3\\ a_3x_1+b_3x_2+c_3x_3\\ \end{bmatrix} \end{aligned} \]
input可以是一个矩阵,例如:
\[ \begin{aligned} &设 \mathbf{X}_{3 \times 2} = (x_{ij})_{i=1,j=1}^{3,2} \\ \mathbf{f}_{3\times 1}(\mathbf{X}) &= \begin{bmatrix} f_1(\mathbf{X})\\ f_2(\mathbf{X})\\ f_3(\mathbf{X}) \end{bmatrix} = \begin{bmatrix} a_1x_{11} + a_2x_{12} + a_3x_{13} + a_4x_{21} + a_5x_{22} + a_6x_{23} \\ b_1x_{11} + b_2x_{12} + b_3x_{13} + b_4x_{21} + b_5x_{22} + b_6x_{23} \\ c_1x_{11} + c_2x_{12} + c_3x_{13} + c_4x_{21} + c_5x_{22} + c_6x_{23} \\ \end{bmatrix} \end{aligned} \]
矩阵function
矩阵function称为实矩阵函数,输出是一个矩阵,使用符号\(\mathbf{F}\)表示,例如有:
\[ \mathbf{F}_{3\times 2} = \begin{bmatrix} f_{11} & f_{12} \\ f_{21} & f_{22} \\ f_{31} & f_{32} \\ \end{bmatrix} \\ \]
input可以是一个标量,例如:
\[ \mathbf{F}_{3\times 2}(x) = \begin{bmatrix} f_{11}(x) & f_{12}(x) \\ f_{21}(x) & f_{22}(x) \\ f_{31}(x) & f_{32}(x) \\ \end{bmatrix} \\ \]
input可以是一个向量,例如:
\[ 设\mathbf{x} = [x_1, x_2, x_3]^T \\ \mathbf{F}_{3\times 2}(\mathbf{x}) = \begin{bmatrix} f_{11}(\mathbf{x}) & f_{12}(\mathbf{x}) \\ f_{21}(\mathbf{x}) & f_{22}(\mathbf{x}) \\ f_{31}(\mathbf{x}) & f_{32}(\mathbf{x}) \\ \end{bmatrix} \\ \]
input可以是一个矩阵,例如:
\[ 设 \mathbf{X}_{3 \times 2} = (x_{ij})_{i=1,j=1}^{3,2} \\ \mathbf{F}_{3\times 2}(\mathbf{X}) = \begin{bmatrix} f_{11}(\mathbf{X}) & f_{12}(\mathbf{X}) \\ f_{21}(\mathbf{X}) & f_{22}(\mathbf{X}) \\ f_{31}(\mathbf{X}) & f_{32}(\mathbf{X}) \\ \end{bmatrix} \\ \]
总结来说可以得到如下的表格:
| function | 标量input | 向量input | 矩阵input |
|---|---|---|---|
| 实值标量函数 | \(f(x)\) | \(f(\mathbf{x})\) | \(f(\mathbf{X})\) |
| 实向量函数 | \(\mathbf{f}(x)\) | \(\mathbf{f}(\mathbf{x})\) | \(\mathbf{f}(\mathbf{X})\) |
| 实矩阵函数 | \(\mathbf{F}(x)\) | \(\mathbf{F}(\mathbf{x})\) | \(\mathbf{F}(\mathbf{X})\) |
矩阵求导以及相关布局
矩阵求导的本质实际上就是function中的每个\(f\)分别对input中的每个元素逐个求偏导,只不过写成了向量、矩阵形式而已。例如考虑实值标量函数,input为向量,即\(f(\mathbf{x}_{n\times 1})\),则有:
\[ \frac{\partial f(\mathbf{x})}{\partial \mathbf{x}_{n\times 1}} = \begin{bmatrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2} \\ ... \\ \frac{\partial f}{\partial x_n} \end{bmatrix} \\ \]
上面我们将结果写成了列向量的形式,当然也可以写成行向量的形式,行列向量的形式互为转置。
\[ \frac{\partial f(\mathbf{x})}{\partial \mathbf{x}_{n\times 1}} = [ \frac{\partial f}{\partial x_1} \frac{\partial f}{\partial x_2} ... \frac{\partial f}{\partial x_n} ] \]
再考虑向量function,同时input也是向量,即\(\mathbf{f}_{m\times1}(\mathbf{x}_{n\times1})\),其中function中有\(m\)个\(f\),input中有\(n\)个元素。进行求导就可以产生\(m\times n\)个结果。这\(m \times n\)个结果如何排列,是写成行向量还是列向量,则对应矩阵求导结果的相关布局。
布局分为分子布局和分母布局。
分子布局指的是分子f是列向量形式,分母x是行向量形式:
\[ \frac{\partial \mathbf{f}_{m\times 1}}{\partial \mathbf{x}_{n \times 1}} = \begin{bmatrix} \frac{\partial f_1}{\partial \mathbf{x}_{n \times 1}} \\ \frac{\partial f_2}{\partial \mathbf{x}_{n \times 1}} \\ ... \\ \frac{\partial f_m}{\partial \mathbf{x}_{n \times 1}} \\ \end{bmatrix} = \begin{bmatrix} \frac{\partial f_1}{\partial x_{1}} & \frac{\partial f_1}{\partial x_{2}} & ... & \frac{\partial f_1}{\partial x_{n}} \\ \frac{\partial f_2}{\partial x_{1}} & \frac{\partial f_2}{\partial x_{2}} & ... & \frac{\partial f_2}{\partial x_{n}} \\ ... \\ \frac{\partial f_m}{\partial x_{1}} & \frac{\partial f_m}{\partial x_{2}} & ... & \frac{\partial f_m}{\partial x_{n}} \\ \end{bmatrix} \\ \]
分母布局指的是分母x是列向量形式,分子f是行向量形式:
\[ \frac{\partial \mathbf{f}_{m\times 1}}{\partial \mathbf{x}_{n \times 1}} = \begin{bmatrix} \frac{\partial \mathbf{f}_{m \times 1}}{\partial x_1} \\ \frac{\partial \mathbf{f}_{m \times 1}}{\partial x_2} \\ ... \\ \frac{\partial \mathbf{f}_{m \times 1}}{\partial x_n} \\ \end{bmatrix} = \begin{bmatrix} \frac{\partial f_{1}}{\partial x_1} & \frac{\partial f_{2}}{\partial x_1} & .. & \frac{\partial f_{m}}{\partial x_1} \\ \frac{\partial f_{1}}{\partial x_2} & \frac{\partial f_{2}}{\partial x_2} & .. & \frac{\partial f_{m}}{\partial x_n} \\ ... \\ \frac{\partial f_{1}}{\partial x_1} & \frac{\partial f_{2}}{\partial x_2} & .. & \frac{\partial f_{m}}{\partial x_n} \\ \end{bmatrix} \\ \]
使用哪种布局并没有严格的要求,只需要前后统一即可。不过无论使用何种布局,\(\mathbf{f}_{m\times1}(\mathbf{x}_{n\times1})\)的导数都是一个二维矩阵,而对于更高维度的矩阵函数,或者输入是矩阵,同样也可以这样分析。此时假设矩阵input的维度为\((a,b)\),那么input中的\(n\)个元素就可以从第一个维度便利,看作是\(a\)个向量,然后依次进行分析,进行推广。
假设此时我们使用分子布局,对于矩阵求导结果的维度则有如下结论:
| function | dim | 标量input | 向量input | 矩阵input |
|---|---|---|---|---|
| dim | \(x(1,)\) | \(\mathbf{x}(n,1)\) | \(\mathbf{X}(n,k)\) | |
| 标量function | \(y(1,)\) | \(\partial y/\partial x(1,)\) | \(\partial y/\partial \mathbf{x}(1,n)\) | \(\partial y/\partial \mathbf{X}(k, n)\) |
| 向量function | \(\mathbf{y}(m,1)\) | \(\partial \mathbf{y}/\partial x(m,1)\) | \(\partial \mathbf{y}/\partial \mathbf{x}(m,n)\) | \(\partial \mathbf{y}/\partial \mathbf{X}(m, k, n)\) |
| 矩阵function | \(\mathbf{Y}(m,l)\) | \(\partial \mathbf{Y}/\partial x(m, l)\) | \(\partial \mathbf{Y}/\partial \mathbf{x}(m, l, n)\) | \(\partial \mathbf{Y}/\partial \mathbf{X}(m, l, k, n)\) |
这里需要注意的是,如果后续没有特别说明,本人笔记中矩阵求导结果默认都使用分子布局,即分子f为列向量形式,分母x为行向量形式。
自动求导
机器学习中非常常用的优化算法是梯度下降法,它的实现关键在于梯度的计算。其中,也会涉及到矩阵求导。下面主要介绍如何进行矩阵导数的计算。
首先回顾标量函数,我们有标量链式法则:
\[ y=f(u),u=g(x),则 \frac{\partial y}{\partial x} = \frac{\partial y}{\partial u} \frac{\partial u}{\partial x} \]
链式法则同样可以推广到向量和矩阵,不过特别需要注意各个阶段的形状:
\[ \begin{aligned} \frac{\partial y}{\partial \mathbf{x}} &= \frac{\partial y}{\partial u} \frac{\partial u}{\partial \mathbf{x}} \\ (1,n)&=(1,)(1,n) \\ \frac{\partial y}{\partial \mathbf{x}} &= \frac{\partial y}{\partial \mathbf{u}} \frac{\partial \mathbf{u}}{\partial \mathbf{x}} \\ (1,n)&=(1,k)(k,n) \\ \frac{\partial \mathbf{y}}{\partial \mathbf{x}} &= \frac{\partial \mathbf{y}}{\partial \mathbf{u}} \frac{\partial \mathbf{u}}{\partial \mathbf{x}} \\ (m,n)&=(m,k)(k,n) \\ \end{aligned} \]
有了推广的链式法则,理论上我们可以进行任何函数的求导。但是神经网络通常具有非常深度的结构,手动进行链式法则求导是比较困难的,因此需要借助自动求导。
自动求导指的是计算一个函数在指定值上的导数,自动求导与符号求导和数值求导不同,符号求导指的是计算出导数的表达式,然后带入特定值直接计算导数值;数值求导指的是利用导数的定义,使用特定值附近差值的极限来计算导数值。
自动求导的思想实际上就是链式法则。对于导数\(\partial y / \partial x\),有:
\[ \frac{\partial y}{\partial x} = \frac{\partial y}{\partial u_n} \frac{\partial u_n}{\partial u_{n-1}} ... \frac{\partial u_2}{\partial u_1}\frac{\partial u_1}{\partial x} \]
通过这个式子,我们可以计算在指定值上的导数。计算方式有两种,分别对应自动求导的两种模式,正向累积和反向累积(其中反向累积就是大名鼎鼎的反向传播Back Propagation,反向传播是用来计算梯度的一种方式)
\[ \begin{aligned} 正向累积: \frac{\partial y}{\partial x} = \frac{\partial y}{\partial u_n} (\frac{\partial u_n}{\partial u_{n-1}}( ... (\frac{\partial u_2}{\partial u_1}\frac{\partial u_1}{\partial x}))) \\ 反向累积:\frac{\partial y}{\partial x} = (((\frac{\partial y}{\partial u_n} \frac{\partial u_n}{\partial u_{n-1}}) ... )\frac{\partial u_2}{\partial u_1})\frac{\partial u_1}{\partial x}) \\ \end{aligned} \]
之后,我们再引入计算图的概念。简单来说,计算图就是将一个计算分解成多步操作,形成一个类似无环图的结构。考虑如下计算图的构造,整个计算图自底向上执行的过程实际上就是计算过程:
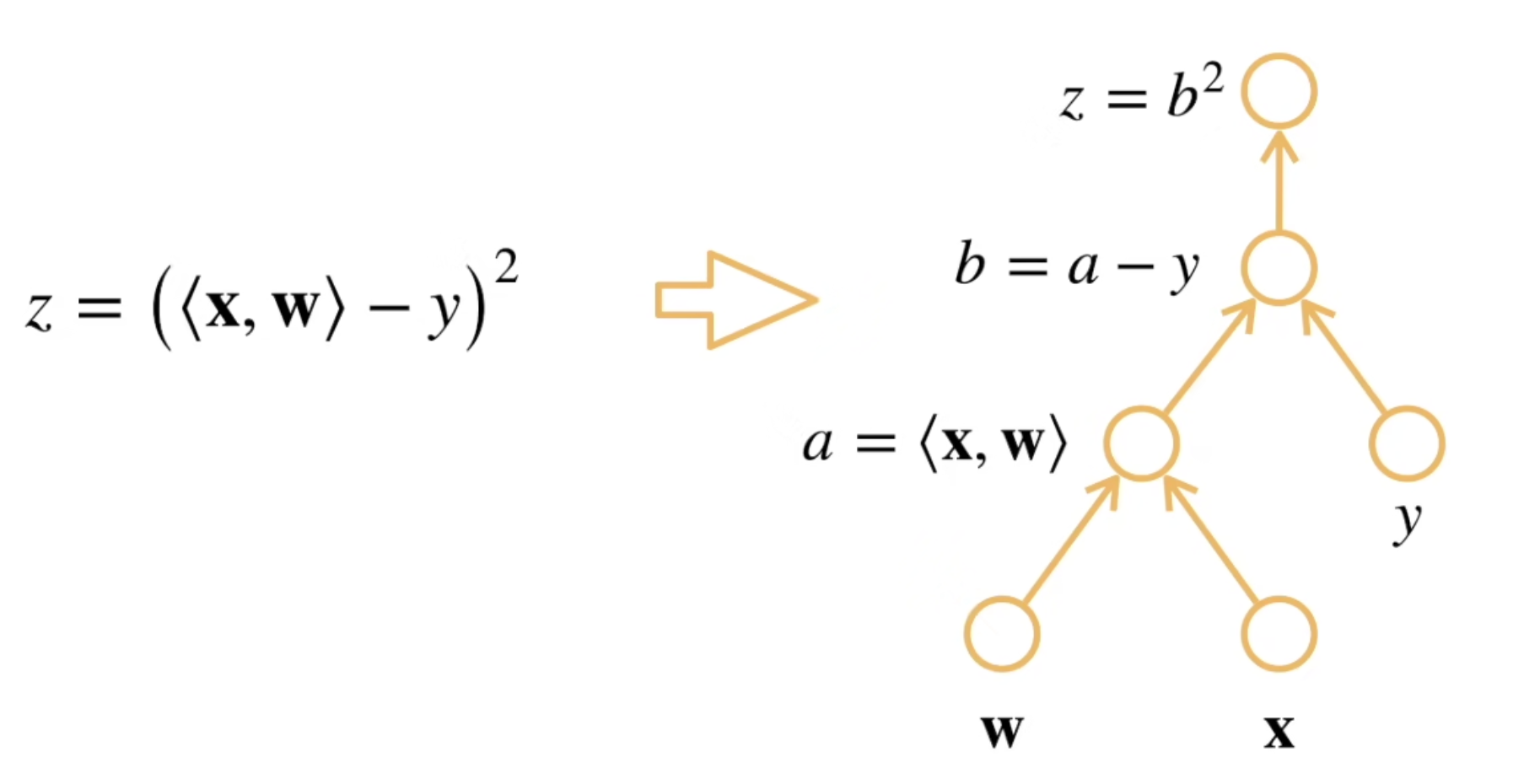
这里我们主要介绍反向累积的计算过程。可以发现,如果结合链式法则,实际上计算图中的每个非叶子节点就是一步计算,可以对应到链式法则中的一次导数计算。
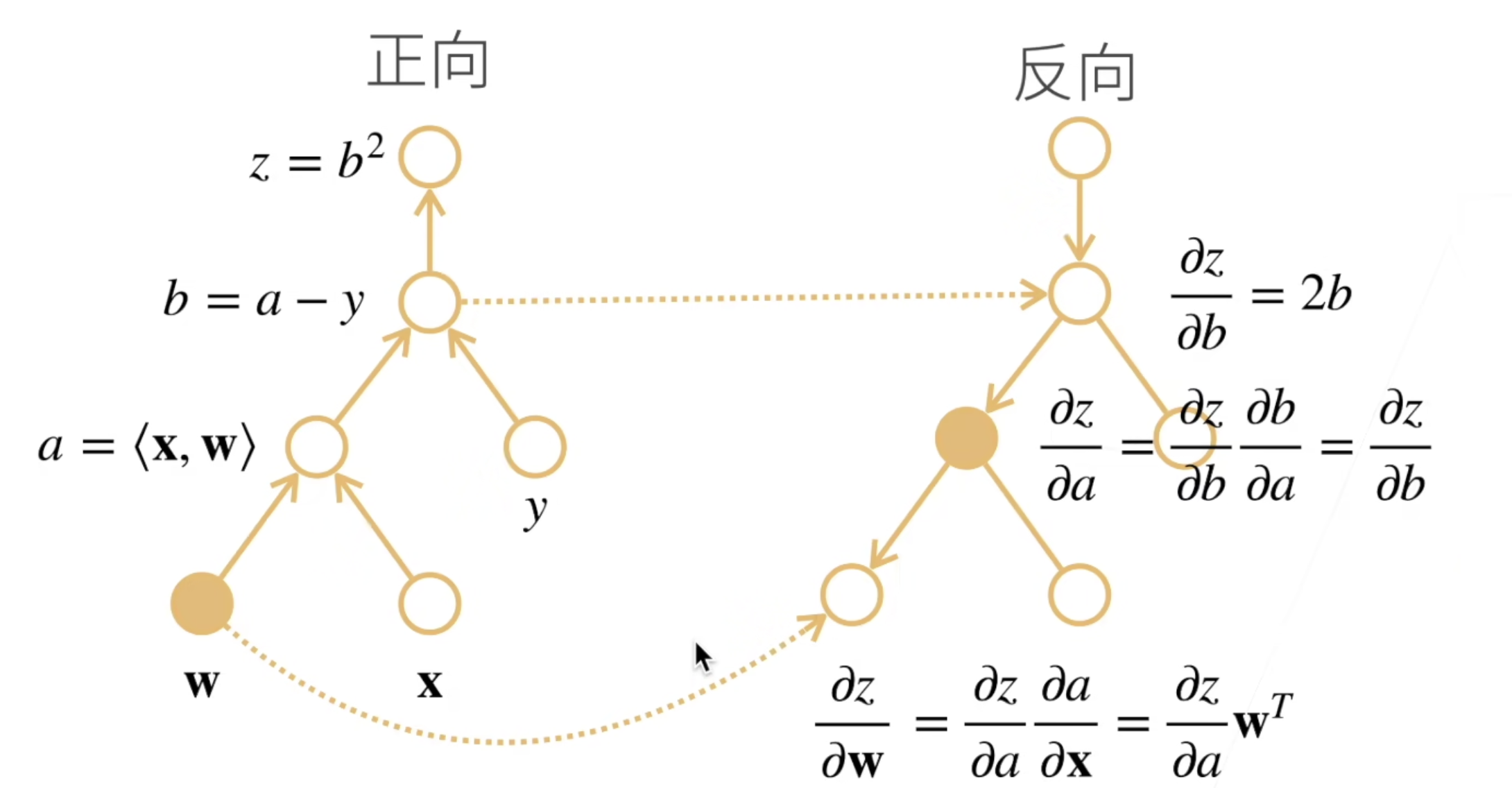
那么为了计算整个导数,我们可以反向执行计算图。即从上到下依次计算各个节点的导数值。举例来说,为了计算\(\partial z / \partial b = 2b\),我们需要知道b的值,即该节点计算过程中的中间结果。
于是整个反向累积的过程实际上分为两个过程:
- 正向过程:自底向上的原式计算过程,需要存储中间结果
- 反向过程:自顶向下的导数计算过程,利用存储的中间结果进行导数计算
如果假设操作子数目为n的话,反向累积的是时间复杂度为\(O(n)\),通常可以认为正向和反向的代价类似;空间复杂度为\(O(n)\),因为需要存储正向过程中的所有中间结果。
在Pytroch中,即利用类似的原理完成自动求导。首先进行数据准备。
1 | |
假设我们现在计算\(\mathbf{x}\)的点积,即:
\[ y = \mathbf{x} \cdot \mathbf{x} = [x_1^2, x_2^2 ,x_3^2, x_4^2] \]
我们可以手动进行符号求导,即
\[ \frac{\partial y}{\partial \mathbf{x}} = [2x_1, 2x_2, 2x_3,2x_4] \]
在Pytroch中,可以通过下面的方式自动计算梯度:
1 | |
我们也可以将\(\mathbf{x}\)的值带入上面进行的手动求导结果中,可以发现确实是相同的。
1 | |
同样我们可以计算其他算式:
1 | |
1 | |
注意这里需要首先对\(y\)进行sum,之后再进行反向传播。这样做是因为在深度学习当中通常考虑的都是标量Loss,因此计算的是标量对向量或矩阵的导数。我们通常不会去计算向量或者矩阵函数的导数,因为这样的Loss维度膨胀会非常快。
并且即使构建函数的计算图需要用过Python控制流,仍然可以计算得到的变量的梯度。这也是隐式构造的优势,因为它会存储梯度计算的计算图,再次计算时执行反向过程就可以。
同时Pytroch还支持将某些计算移动到计算图之外,即不计算这部分的梯度。这种方式可以用于将神经网络的一些参数进行固定:
1 | |
CUDA、GPU以及相关概念厘清
相关概念
在深度学习相关框架中,我们基本避不开GPU显卡的使用,但是在使用的过程中,经常会遇到例如显卡驱动、Cuda Driver、Cuda、cuda-toolkit、cudann等等相关概念。下面我们就对这些概念进行一个统一的说明:
- 显卡:可以理解为我们通常所说的GPU,由于NVIDIA公司的GPU芯片占据了大部分市场份额,深度学习中使用的几乎都是NVIDIA的GPU
- 显卡驱动:通常指的是NVIDIA Driver,GPU是硬件,而它则是驱动软件,表现为一个经典nvidia绿色,可以登陆账号的软件。
- CUDA:全称为Compute Unified Device Architecture,它是一个并行计算平台和编程模型,能够使得使用GPU进行通用计算变得简单和优雅。它允许开发者使用NVIDIA GPU进行通用计算,同时提供了一个扩展编程接口,使开发可以直接在GPU上编写代码。
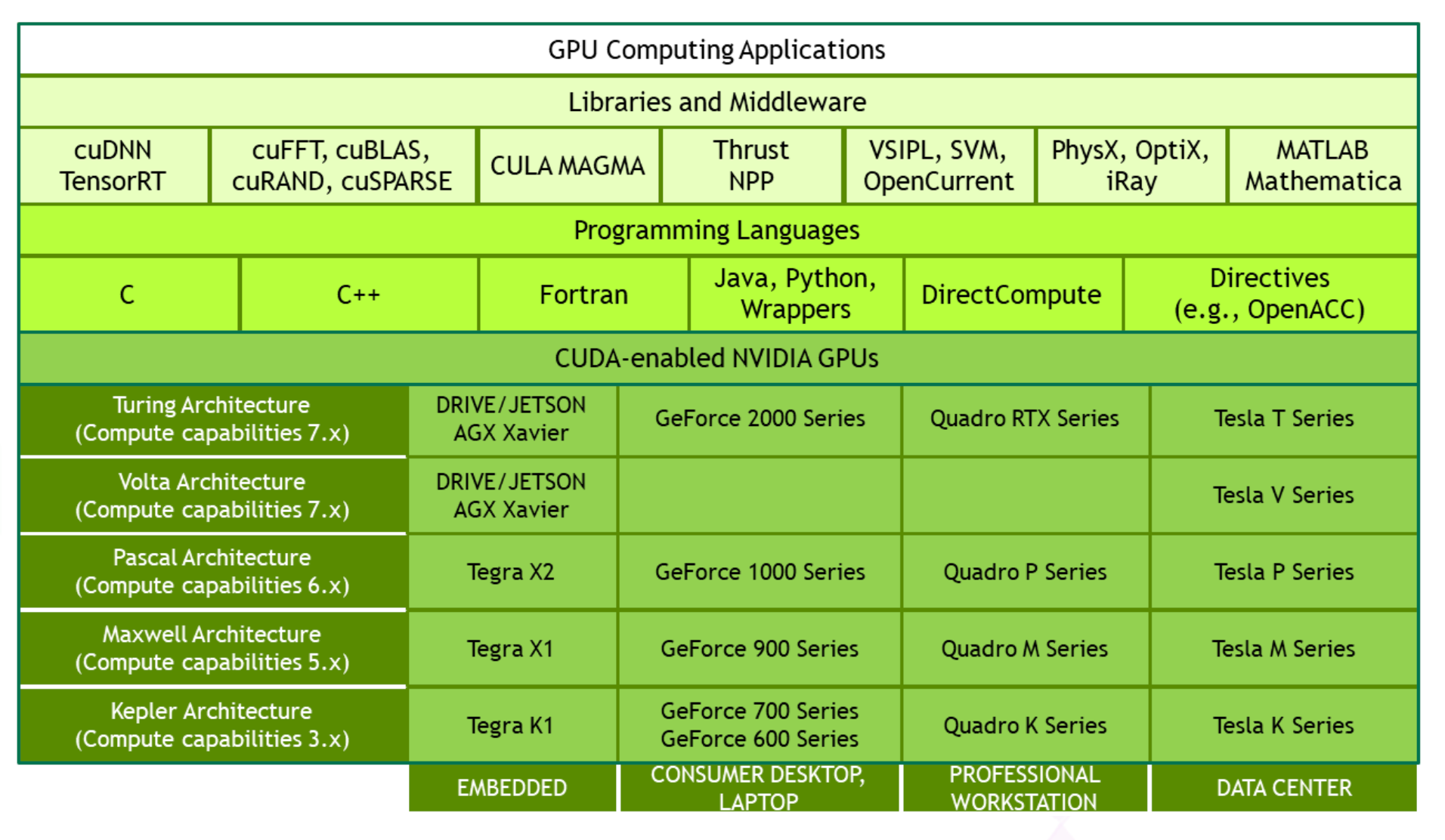
- cudnn:nvidia提供的专门为深度学习计算而设计的软件库,里面提供了很多专门的计算函数,例如卷积操作等,用于对深度学习网络进行加速
- 如上图所示,cudnn属于library级别。还有许多其他的软件库和中间件,包括实现C++ STL的Thrust、实现GPU版本BLAS的cublas(高性能线性代数计算)、实现快速傅立叶变换的cuFFT、实现稀疏矩阵运算操作的cuSparse等
- CUDA Toolkit:CUDA
Toolkit是nvidia提供的开发工具包,也就是我们常说的带版本的cuda(cuda11.7、cuda11.8、cuda12.1...)。它包括编译器、运行时库、CUDA核心核心、API、样例代码和开发工具等,帮助开发者利用CUDA技术来编写应用程序:
- Compiler:CUDA-C和CUDA-C++的编译器
nvcc,它位于bin/目录下。nvcc之于cuda程序就类似于gcc之于c程序,g++之于c++程序。 - Tools:提供一些类似profiler、debuggers等的工具,这些工具也可以从
bin/目录下获取 - Libraries:提供相关的科学库和程序库文件,可以在
lib/目录下找到,头文件可以在include/目录中找到。实际上这些库文件就是一系列静态链接库和动态链接库,头文件就是一系列.h文件- cudart: CUDA Runtime
- cudadevrt: CUDA device runtime
- cupti: CUDA profiling tools interface
- nvml: NVIDIA management library
- nvrtc: CUDA runtime compilation
- cublas: BLAS (Basic Linear Algebra Subprograms,基础线性代数程序集)
- cublas_device: BLAS kernel interface
- CUDA Samples:演示如何使用各种CUDA和Library
API的代码示例,在
samples/目录中存放
- Compiler:CUDA-C和CUDA-C++的编译器
- CUDA Driver:驱动程序本身是操作系统与硬件之间的接口,而CUDA Driver是操作系统与NVIDIA GPU之间的接口,提供了对GPU硬件的低级别控制。它需要独立安装,负责管理GPU资源和执行CUDA代码的低级别操作
- CUDA Runtime:它是一个高层API,位于CUDA Driver之上。它包含在CUDA Toolkit中,通常会与特定版本的CUDA一起安装。开发者编写的CUDA程序主要都是通过高级API CUDA Runtime来和GPU进行交互,而不是直接使用CUDA Driver
CUDA安装
假设我们已经有了显卡,想利用它进行深度学习程序的运行,那么就需要安装CUDA,也就是上面CUDA
Toolkit的安装。安装只需要进入官方网站CUDA Toolkit
Downloads根据操作系统等信息来选择下载相关的文件(例如.run),之后运行文件即可。根据引导指示安装完成之后,需要修改.bashrc配置文件,主要是为了将CUDA
Toolkit的bin目录和库目录lib加入对应的环境变量中,类似于:
1 | |
这里的环境变量LD_LIBRARY_PATH表示程序加载运行期间查找动态链接库时,除了系统默认路径之外的其他路径。由于CUDA的动态链接库存放在lib/(or
lib64/)目录下,要想在运行的时候要找到这些动态链接库,就需要将其添加到对应的环境变量中。