动手学深度学习(2)-线性模型

线性回归

简介

这里对于线性回归不做详细的介绍，更加详细的介绍可以参考本人的其他相关笔记：机器学习基础(6)线性回归与Logistic回归|EverNorif。

线性回归模型如下，其中，对于单个输入向量\(\mathbf{x}\)，使用\(\hat{y}\)来表示预测值，\(\mathbf{w},b\)表示模型的参数： \[ \hat{y} = \mathbf{w}^T \mathbf{x} + b \] 对于批量的输入，则可以按照列向量的形式将其组织成矩阵： \[ \mathbf{X} = \begin{bmatrix} \mathbf{x_1} \\ \mathbf{x_2} \\ ... \\ \mathbf{x_n} \end{bmatrix} \] 则有：

\[ \hat{\mathbf{y}} = \mathbf{X}\mathbf{w} + b \]

损失函数通常使用均方误差： \[ \text{loss}(\mathbf{w}, b) = \frac{1}{2} (y - \hat{y})^2 \] 优化目标最小化下面的总损失： \[ L(\mathbf{w}, b) = \frac{1}{n} \sum_{i=1}^{n} \frac{1}{2}(\mathbf{w}^T \mathbf{x}^{(i)} + b - y^{(i)})^2 \] 优化方法使用mini-batch随机梯度下降。

代码实现

下面将从零开始实现线性回归。（当然不是完完全全从基础开始实现，而是借助pytorch中的部分基础API来完成，包括Tensor和自动微分等）

首先我们需要构造一些测试数据。在测试数据中，引入噪声使得数据更加真实。其中\(X\)代表批量输入，行数为输入的向量个数，列数为向量维度。

1
2
3
4
5
6
7
8
9
def synthetic_data(w, b, num_examples):  # num_examples表示样本个数
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)  # 模拟噪声
    return X, y.reshape((-1, 1))  # -1 表示自动计算相应维度

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

在训练过程中我们需要使用mini-batch随机梯度下降，因此这里实现一个能够按照batch_size进行数据随机提取的方法：

1
2
3
4
5
6
7
8
9
10
import random


def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)  # 随机shuffle
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])  # 防止越界
        yield features[batch_indices], labels[batch_indices]  # 使用tensor的index矩阵取值

接下来完成模型和损失函数的定义，模型即为简单的线性回归，注意这里的模型接收的是批量的feature

1
2
def linear_regression(X, w, b):
    return torch.matmul(X, w) + b

损失函数就是均方误差：

1
2
def squared_loss(y_hat, y):
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

同时还需要完成优化算法，mini-batch随机梯度下降的定义，其中params表示需要更新的参数，实际上就对应了这里的\(\mathbf{w},b\)：

1
2
3
4
5
def sgd(params, learning_rate, batch_size):
    with torch.no_grad():
        for param in params:
            param -= learning_rate * param.grad / batch_size
            param.grad.zero_()

之后就可以进行训练过程了。我们首先对必要的参数进行初始化，包括随机初始化模型参数，以及指定一些超参数例如learning_rate，epochs，batch_size等。这里我们将整个训练过程进行一定程度的抽象，例如net和loss，使得后续的相关模型也可以使用：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 模型参数初始化
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# 超参数初始化
learning_rate = 0.03
num_epochs = 5
batch_size = 10
# model和loss
net = linear_regression
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  # 前向传播
        l.sum().backward()  # 反向传播
        sgd([w, b], learning_rate, batch_size) # 参数更新
    with torch.no_grad():  # 每个epoch输出一次loss，此时不需要更新梯度
        train_loss = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss: {float(train_loss.mean())}')

由于测试数据是我们构造出来的，因此可以查看训练出的参数和真实的参数之间的差距：

1
2
print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

输出如下，可以看到还是比较接近的。

1
2
w的估计误差: tensor([-0.0001,  0.0002], grad_fn=<SubBackward0>)
b的估计误差: tensor([0.0002], grad_fn=<RsubBackward1>)

pytorch实现

上面的过程如果利用Pytorch，实际上有更为简洁的实现。

首先测试数据的准备和上面是一样的，即：

1
2
3
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

之后需要进行数据加载的准备，数据加载使用到了Pytorch中的Dataset和DataLoader相关API。这里的is_train表示是否需要对数据进行shuffle。此时返回的DataLoader对象实际上和上面的data_iter有着相同的使用方式：

1
2
3
4
5
6
import torch
from torch.utils import data

def load_array(data_arrays, batch_size, is_train=True):
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

之后需要定义模型，线性模型在Pytroch中有着非常简单的定义方式，其中构造方法中的两个参数分别表示输入维度和输出维度，在示例的情况下就是2和1：

1
2
3
from torch import nn

net = nn.Sequential(nn.Linear(2, 1))

均方误差和优化算法同样有所提供，其中MSELoss默认情况下返回所有样本损失的平均值：

1
2
loss = nn.MSELoss()
trainer = torch.optim.SGD(net.parameters(), lr=learning_rate)

这里我们可以通过手动指定来初始化模型参数：

1
2
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)

之后就可以开始训练了：

1
2
3
4
5
6
7
8
9
10
11
12
num_epochs = 5
batch_size = 10
data_iter = load_array((features, labels), batch_size)

for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X), y)  # 前向传播
        trainer.zero_grad()
        l.backward()  # 反向传播
        trainer.step()  # 参数更新
    train_loss = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss: {train_loss:f}')

最后同样可以得到相关参数，查看差距：

1
2
3
4
w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)

输出如下：

1
2
w的估计误差： tensor([-0.0005, -0.0005])
b的估计误差： tensor([-0.0007])

不过需要注意的是，我们关注的从来不是预测模型的参数和真实参数的差距，因为真实参数往往是不知道的，并且真实模型也是非常复杂的。我们最终关心的是模型的预测效果。

Softmax回归

简介

同样首先对softmax回归做一个简单描述，该模型解决的是一个多分类问题。

softmax回归模型如下，其中，对于单个输入向量\(\mathbf{x}\)，使用\(\hat{\mathbf{y}}\)来表示预测值，这是一个一定维度的向量，维度指等于预测类别的总数，\(\mathbf{W},\mathbf{b}\)表示模型的参数。这里的\(\mathbf{W}\)是一个矩阵， \[ \hat{\mathbf{y}} = \text{softmax}(\mathbf{W}^T \mathbf{x} + \mathbf{b}) \] 同样我们需要将其扩展到对于批量的输入，通常我们都是在第一个维度上进行批量的叠加。假设特征的维度为\(d\)，批量的大小为\(n\)，多分类的类别数量为\(q\)，那么有，注意各个参数的shape，这里有广播机制的参与： \[ \begin{aligned} \mathbf{O}_{(n,q)} &= \mathbf{X}_{(n, d)}\mathbf{W}_{(d,q)} + \mathbf{b}_{(1, q)} \\ \hat{\mathbf{Y}}_{(n,q)} &= \text{softmax}(\mathbf{O}_{(n,q)}) \end{aligned} \] 这里的softmax按照第一个维度也就是按照行进行执行。

损失函数使用交叉熵损失Cross Entropy，这里的真实target \(\mathbf{y}\)是一个one-hot向量： \[ loss(\mathbf{y}, \hat{\mathbf{y}}) = - \sum_{j=1}^q y_i \log \hat{y_i} \] 于是优化目标为最小化下面的总损失： \[ L(\mathbf{W}, \mathbf{b}) = \sum_{i=1}^n loss(\mathbf{y}^{(i)}, \hat{\mathbf{y}}^{(i)}) \]

代码实现

这里我们选择FashionMNIST数据集来作为图像分类的测试。FashionMNIST包含10个类别的图像，每个类别都包含作为训练集的6000张图片以及作为测试集的1000张图像。整个数据集包含70000张图像，每张图片都是\(1 \times28 \times 28\)的灰度图像。

通过torchvision提供的API获取，得到的是Dataset对象。

1
2
3
4
5
6
import torch
import torchvision
from torchvision import transforms

mnist_train = torchvision.datasets.FashionMNIST(root='./data', train=True, transform=transforms.ToTensor(), download=True)
mnist_test = torchvision.datasets.FashionMNIST(root='./data', train=False, transform=transforms.ToTensor(), download=True)

Fashion-MNIST中包含的10个类别，分别为t-shirt（T恤）、trouser（裤子）、pullover（套衫）、dress（连衣裙）、coat（外套）、sandal（凉鞋）、shirt（衬衫）、sneaker（运动鞋）、bag（包）和ankle boot（短靴）。 以下函数用于在数字标签索引及其文本名称之间进行转换。

1
2
3
def get_fashion_mnist_labels(labels):
    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat', 'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    return [text_labels[int(i)] for i in labels]

为了进行批量数据读取，我们需要将Dataset包装为DataLoader并进行返回。下面的函数包装好了数据加载的全流程，返回的是训练和测试的DataLoader对象，其中resize表示是否需要对图像进行形状变换：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import torch
import torchvision
from torch.utils import data
from torchvision import transforms


def load_data_fashion_mnist(batch_size, path='./data', resize=None, num_workers=4):
    trans = [transforms.ToTensor()]
    if resize:
        trans.insert(0, transforms.Resize(resize))
    trans = transforms.Compose(trans)
    mnist_train = torchvision.datasets.FashionMNIST(root=path, train=True, transform=trans, download=True)
    mnist_test = torchvision.datasets.FashionMNIST(root=path, train=False, transform=trans, download=True)
    return (data.DataLoader(mnist_train, batch_size, shuffle=True, num_workers=num_workers),
            data.DataLoader(mnist_test, batch_size, shuffle=False, num_workers=num_workers))

在准备好数据之后，需要进行模型的构建。相比于线性回归，softmax回归多出了一层softmax，因此实现如下：

1
2
3
4
5
6
7
def softmax(X):
    X_exp = torch.exp(X)
    partition = X_exp.sum(1, keepdim=True)
    return X_exp / partition

def softmax_regression(X, W, b):
    return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)

之后需要定义交叉熵损失函数。

1
2
def cross_entropy(y_hat, y):
    return - torch.log(y_hat[range(len(y_hat)), y])

注意这里交叉熵损失的实现和我们实际问题场景是对应的。首先对于每一个输入来说，我们这里的真实target y并不是一个one-hot向量，而是一个0-9的数值。批量化处理之后，这里的y_hat就是一个\((n,q)\)的矩阵，表示\(n\)个长度为\(q\)的向量，该向量表示对\(q\)个类别分别的概率预测。而y则是一个\((n,)\)的向量，每个数值分别表示对应的真实target。因此这里实际用到了tensor的index矩阵取值方式。对于输入矩阵的第\(i\)个向量，假设它对应的真实target为j，那么要计算预测向量和真实target one hot向量的交叉熵的话，实际上只需要找到预测向量中的第\(j\)个元素即可，因为target one hot向量的其他值都是0，并且由于不为0的位置上是1，因此log前的系数也可以省略。同时这里使用pytorch中的向量化，做到了逐元素计算。

交叉熵损失是用来优化模型的损失函数，我们当然可以用它来评估训练的效果，不过还有其他常用的指标，例如对于分类问题来说，可以使用accuracy，即分类正确的个数占总数的比例，计算方式如下（注意这里同样要结合真实的target情况来看）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def accuracy(y_hat, y):  # 计算y_hat中预测正确的个数
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    cmp = y_hat.type(y.dtype) == y
    return float(cmp.type(y.dtype).sum())

def evaluate_accuracy(net, data_iter, W, b): # 计算在整个数据上的正确率，需要累积正确数目和总数
    correct_num, all_num = 0.0, 0.0
    with torch.no_grad():
        for X, y in data_iter:
            y_hat = net(X, W, b)
            correct_num += accuracy(y_hat, y)
            all_num += y.numel()
    return correct_num / all_num

这里使用了一个我们实现的累加器，初始化时指定需要存储多少个累加值，之后在使用过程中逐步累加。

1
2
3
4
5
6
7
8
9
10
11
12
class Accumulator:
    def __init__(self, n):
        self.data = [0.0] * n

    def add(self, *args):
        self.data = [a + float(b) for a, b in zip(self.data, args)]

    def reset(self):
        self.data = [0.0] * len(self.data)

    def __getitem__(self, idx):
        return self.data[idx]

之后完成参数的初始化指定，就可以进行训练了。这里的num_inputs表示第一层输入需要将二维矩阵拉平，转化为一维向量。优化方法仍然沿用之前的SGD。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
num_epochs = 10
learning_rate = 0.1
batch_size = 100

num_inputs = 28 * 28
num_outputs = 10

W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)

train_data_loader, test_data_loader = load_data_fashion_mnist(batch_size)
net = softmax_regression
loss = cross_entropy

for epoch in range(num_epochs):
    metric = Accumulator(3) # 累积一个epoch的损失（loss, correct_num, all_num）
    for X, y in train_data_loader:
        y_hat = net(X, W, b)
        l = loss(y_hat, y)
        l.sum().backward()
        sgd([W, b], learning_rate, batch_size)

        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())

    training_loss = metric[0] / metric[2]
    training_accuracy = metric[1] / metric[2]

    print(f"epoch {epoch + 1}, loss: {training_loss}")
    print(f"epoch {epoch + 1}, accuracy: {training_accuracy}")

在训练完成之后，可以评估一下模型在测试集上的效果：

1
2
3
4
5
6
7
8
9
10
metric = Accumulator(3)
for X, y in test_data_loader:
    y_hat = net(X, W, b)
    l = loss(y_hat, y)
    metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())

test_loss = metric[0] / metric[2]
test_accuracy = metric[1] / metric[2]
print(f"loss: {test_loss}")
print(f"accuracy: {test_accuracy}")

pytorch实现

下面利用Pytorch中更简洁的实现。

DataLodaer沿用上面的数据加载方式。

模型定义如下，并完成参数初始化：

1
2
3
4
5
6
7
8
9
10
11
from torch import nn

num_inputs = 28 * 28
num_outputs = 10

net = nn.Sequential(nn.Flatten(), nn.Linear(num_inputs, num_outputs))

def init_weights(layer):
    if type(layer) == nn.Linear:
        nn.init.normal_(layer.weight, std=0.01)
net.apply(init_weights)

损失函数沿用交叉熵损失：

1
loss = nn.CrossEntropyLoss()

优化器仍然沿用SGD：

1
2
learning_rate = 0.1
optimizer = trainer=torch.optim.SGD(net.parameters(),lr=learning_rate)

之后进行训练，注意代码与上面的区别：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
num_epochs = 10
batch_size = 256

train_data_loader, test_data_loader = load_data_fashion_mnist(batch_size)

for epoch in range(num_epochs):
    metric = Accumulator(3) # 累积一个epoch的损失（loss, correct_num, all_num）
    for X, y in train_data_loader:
        y_hat = net(X)
        l = loss(y_hat, y)

        optimizer.zero_grad()
        l.mean().backward()
        optimizer.step()

        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())

    training_loss = metric[0] / metric[2]
    training_accuracy = metric[1] / metric[2]

    print(f"epoch {epoch + 1}, loss: {training_loss}")
    print(f"epoch {epoch + 1}, accuracy: {training_accuracy}")

同样可以进行测试：

1
2
3
4
5
6
7
8
9
10
metric = Accumulator(3)
for X, y in test_data_loader:
    y_hat = net(X)
    l = loss(y_hat, y)
    metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())

test_loss = metric[0] / metric[2]
test_accuracy = metric[1] / metric[2]
print(f"loss: {test_loss}")
print(f"accuracy: {test_accuracy}")

总结

通过对线性回归和Softmax回归的从零手动实现和代码实现，我们可以发现模型训练过程中的一些基本要素，包括DataLoader、Model、Loss和Optimizer。这些要素实际上也就是最重要的模块。也可以参考Pytorch快速入门 - EverNorif中的Quick Start，其中就描述了模型训练的基本过程。

补充说明

softlabel策略

我们说对于分类的target，一种方法是将其表示为one hot向量，此时的one hot向量可以理解为概率向量，对应位置上表示属于哪一类。这样考虑有三种类别，如果属于第二类的话，target one hot向量就是\((0, 1, 0)\)。

softlabel策略指的是我们不需要完全将概率限定到1，而是把它修改成一个非常高的概率，例如上面的例子，如果使用softlabel策略的话，可以表示为\((0.05, 0.9, 0.05)\)。

softlabel策略实际上是一个常用的小技巧，softmax中含有指数，逼近1是非常困难的事情，但是逼近一个非常接近1的数值还是可以做到的，因此softlabel策略实际上就是使得结果逼近变得可能。

损失函数设计思路探寻

在机器学习的过程中，我们定性描述所做的工作就是，在理论世界中有一个模型，它可以绝对正确地完成所需要完成的工作（如预测，分类等等），我们希望得到在现实世界的另一个模型，也能完成这项工作。而理论世界中的模型很复杂很抽象，我们无法精确地用定量的方式来描述，我们有的只是理论模型工作的结果（如分类的标签值，这也就是训练集）。我们是利用这些结果来构造现实世界的模型。

得到了现实世界的模型，我们当然想知道它和理论模型有多接近。于是我们就需要设计某个东西来衡量这两个模型的接近性（相似性），也就是衡量我们得到的现实模型效果如何，并且希望是能够定量地描述这个效果。我们是利用损失函数来完成这一项工作。前面所说，损失函数是用来衡量一组参数好坏的。在机器学习的过程中，我们是通过让损失函数的值达到最小，来确定现实模型。

那损失函数是如何设计的呢？它有三种思路：最小二乘法，极大似然估计法和交叉熵法。

（下面的内容有统一的符号规定：\(\hat{y_i}\)表示对于第i个输入，机器的输出值；\(y_i\)表示对于第i个输入，它的真实值label）

最小二乘法

既然要比较两个模型之间的接近性，也即比较两个模型的差距，一个很直观的想法就是去利用它们产生的结果，也就是\(y_i\)和\(\hat{y_i}\)​​。而事实上，我们也无法利用其它参数来进行比较。（假设理论模型可以用一组参数来完全确定，但就算如此这组参数我们也是未知的）

比较产生的结果，我们自然而然又可以想到下面： \[ \begin{aligned} \text{衡量结果的差距：} &\sum_i|y_i-\hat{y_i}| \\ \text{绝对值函数并非处处可导，于是改进：} &\sum_i(y_i-\hat{y_i})^2 \\ \text{希望两者的差距最小：}& \min{\sum_i(y_i-\hat{y_i})^2} \\ \text{损失函数设计为：}&\sum_i(y_i-\hat{y_i})^2 \\ \end{aligned} \] 而这也就是最小二乘法的思想。

极大似然估计法

理论世界的模型和现实世界的模型，我们也可以将它看作是概率模型。在分类的问题当中，理想情况下，我们希望现实模型的输出\(y_i\)是一个概率值，即属于某个类别的概率。而利用极大似然估计的思想，即为出现样本的概率最大。

对于一个二分类的问题，输出值\(\hat{y_i}\)表示输入对应\(y_i=1\)的概率；自然有输入对应\(y_i=0\)的概率为\(1-\hat{y_i}\)​（对应一个伯努利分布）: \[ \begin{aligned} \text{假设样本i对应label=1,样本出现概率为:}&\hat{y_i} \\ \text{假设样本i对应label=0,样本出现概率为:}&1-\hat{y_i} \\ \text{二者统一表达，对于任意样本i，出现概率为:}&\hat{y_i}^{y_i}(1-\hat{y_i})^{1-y_i} \end{aligned} \] 极大似然法就是要让所有样本出现的几率变得最大： \[ \max{\prod_i\hat{y_i}^{y_i}(1-\hat{y_i})^{1-y_i}} \] 这个式子也可以做下面的一些等价变换： \[ \begin{aligned} &\prod_i\hat{y_i}^{y_i}(1-\hat{y_i})^{1-y_i} \\ &\log{\prod_i\hat{y_i}^{y_i}(1-\hat{y_i})^{1-y_i}}\\ =&\sum_i [y_i\log{\hat{y_i}} + (1-y_i)\log{(1-\hat{y_i})}] \end{aligned} \] 于是： \[ \begin{aligned} &\max{\prod_i\hat{y_i}^{y_i}(1-\hat{y_i})^{1-y_i}}\\ &\max{\sum_i [y_i\log{\hat{y_i}} + (1-y_i)\log{(1-\hat{y_i})}}]\\ &\min{-\sum_i [y_i\log{\hat{y_i}} + (1-y_i)\log{(1-\hat{y_i})}}] \end{aligned} \]

交叉熵法

首先回归我们的目标，比较理想模型和现实模型。对于两个概率模型来说，如果这两个概率模型的类型相同，我们可以通过比较参数来比较这两个模型；但是如果这两个模型类型不相同，我们就无法通过参数来进行比较。熵就是一个用来解决这个问题的办法。对于任何的概率模型，我们都可以计算出它的熵，然后通过比较不同概率模型的熵，我们就可以来比较两个概率模型。

首先我们需要引入信息量的概念。所谓信息量，是给我们带来确定性的。如果一件事情由不确定变成了确定的，那它就给我们带来了信息量。并且我们可以说，信息量衡量的是从不确定变成确定的难度。而既然说到了不确定性，当然应该和概率有关系。在这里，我们假设函数\(f\)来表示信息量，并且在本节的下面篇幅中，\(f\)均代表信息量的计算： \[ f(x):= \text{信息量} \] 考虑下面的图：

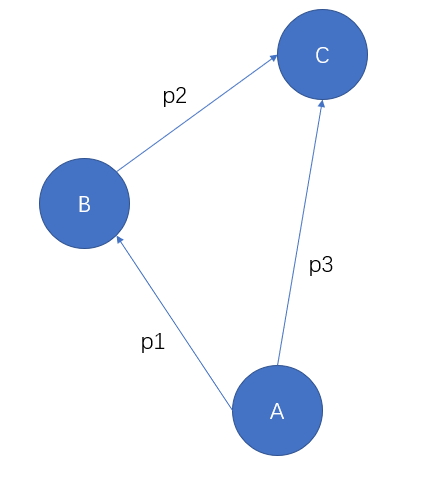
从事件A到事件C，有\(p_3\)的概率；从事件A到事件B，有\(p_1\)的概率；从事件B到事件C，有\(p_2\)的概率。

如果最终从事件A到了事件C，那么无论是从什么路径到达的，它带来的信息量应该是一样多的，并且结合概率公式，应该有如下条件： \[ \begin{aligned} f(p_3) &= f(p_1)+f(p_2)\\ p_3 &= p_1 \times p_2 \end{aligned} \] 因为\(f\)需要满足上面的式子，我们可以定义它使用log： \[ f(x):=?\log_?x \] 这样还需要确定系数和底数。对于信息量来说，这里的x表示的是事件发生的概率。越小概率的事件，如果发生了对应的信息量应该越大，函数\(f\)应该是一个递减函数，于是我们将系数定义为-1。此时我们可以做到自洽，底数的选择并不会影响后续逻辑。（这里选择底数为2）

这样信息量的表达式最终就写成： \[ f(x):=-log_2x \] 接下来考虑的就是熵的定义。信息量考虑的是一个事件，而熵考虑的是一个系统内的所有事件（式子中的\(P\)​指的是在一个概率系统当中）。 \[ H(P):=\text{熵} \] 假设一个系统内可能发生事件\(X,Y,Z\)​，他们发生的概率分别为\(p_1,p_2,p_3\)​。由上面我们知道，他们对应的信息量为\(f(p_1),f(p_2),f(p_3)\)。但是信息量指的是一个事件发生之后带来的，如果事件没有发生，就没有这么多信息量。所以系统的熵不应该是各事件信息量的简单加和，而应该结合对应事件的概率： \[ \begin{aligned} H(P=\{ X:p_1,Y:p_2,Z:p_3\}) &:=p_1f(p_1)p_2f(p_2)p_3f(p_3)\\ &=p_1(-log_2p_1)+p_3(-log_2p_2)+p_3(-log_2p_3) \end{aligned} \] 于是，对于一个概率系统\(P\)来说，熵即为对概率系统中的信息量求期望： \[ \begin{aligned} H(P) &:= E(P_f)\\ &=\sum_i p_if(p_i) \\ &=\sum_ip_i(-log_2p_i) \\ &=-\sum_ip_i \cdot log_2p_i \end{aligned} \] 现在有了熵的定义，要比较两个概率模型，直接比较熵还是太简单粗暴了，于是下面引入相对熵的概念。

相对熵，也叫KL散度。它比较的是两个概率模型\(P\)​和\(Q\):

这是对离散型随机变量而言的，如果是连续型的随机变量，则需要改求和为积分 \[ \begin{aligned} KL(P||Q) &= \sum P(x)\log \frac{P(x)}{Q(x)} \\ KL(P||Q) &= \int P(x)\log \frac{P(x)}{Q(x)}dx \end{aligned} \]

\[ \begin{aligned} D_{KL}(P||Q) &:= \sum_i p_i \cdot(f_Q(q_i)-f_P(p_i)) \\ &=\sum_i p_i \cdot((-log_2q_i)-(-log_2p_i)) \\ & = \sum_i p_i(-log_2q_i) - \sum_ip_i(-log_2p_i) \end{aligned} \]

公式中\(P\)在前，表示以\(P\)为基准，去比较\(Q\)和\(P\)相差多少。在式子中，后面一项正好是\(P\)的熵；而前面一项就是\(P\)和\(Q\)​​的交叉熵\(H(P,Q)\)。这两项越接近，相对熵越接近0，表示两个概率模型越接近。

而因为有吉布斯不等式： \[ \begin{aligned} &\text{如果} \sum_{i=1}^np_i = \sum_{i=1}^nq_i = 1,\text{且}p_i,q_i \in (0,1],\text{则有：}\\ &-\sum_{i=1}^np_i\log p_i \le -\sum_{i=1}^nq_i \log q_i \\ &\text{等号成立当且仅当 }\forall i,p_i = q_i \end{aligned} \] 所以我们可以确定相对熵是大于等于0的。这样也就说明交叉熵越小，表示两个概率模型越接近。

下面需要考虑的是如何将交叉熵应用到实际的机器学习中。同样考虑二分类问题，

对于一个二分类的问题，输出值\(\hat{y_i}\)表示输入对应\(y_i=1\)的概率；自然有输入对应\(y_i=0\)的概率为\(1-\hat{y_i}\)（对应一个伯努利分布）: \[ \begin{aligned} \text{假设样本i对应label=1,样本出现概率为:}&\hat{y_i} \\ \text{假设样本i对应label=0,样本出现概率为:}&1-\hat{y_i} \end{aligned} \] 应用到实际输出： \[ \begin{aligned} H(P,Q) &=\sum_i p_i(-\log_2 q_i) \\ &=\sum_i y_i(-\log_2 q_i) \\ &=-\sum_i [y_i\cdot \log_2 \hat{y_i} +(1-y_i)\log_2(1-\hat{y_i})] \\ \end{aligned} \] 这里从\(q_i\)到\(\hat{y_i}\)的对应需要说明一下，交叉熵中，\(P\)和\(Q\)应该是对应同一件事情的概率，因此这里在\(y_i\)不同的情况下，应该分开考虑。

交叉熵越小，代表两个模型越相似，所以我们希望的也是最小化这个交叉熵： \[ \min{-\sum_i [y_i\cdot \log_2 \hat{y_i} +(1-y_i)\log_2(1-\hat{y_i})]} \] 得到和极大似然估计法相同的式子。

交叉熵法和极大似然估计法，最后得到的表达式是相同的，但是意义不同。

极大似然法中，log是由于改连乘为连加而引入的，负号是因为我们习惯求最小值而引入的；

交叉熵法中，log和负号都是写在定义里面的。

深度学习 > 动手学深度学习
#深度学习
动手学深度学习(2)-线性模型
http://example.com/2023/08/29/动手学深度学习-2-线性模型/
作者
EverNorif
发布于
2023年8月29日
许可协议