Games101(1)-线性代数基础与变换
线性代数基础
该部分可以首先参考线性代数的本质 - EverNorif,其中以直观地方式介绍了线性代数的几何意义。
在图形学中涉及的线性代数,主要可以分为两大部分,分别是向量和矩阵,下面将简单介绍相关概念。
向量Vector
向量之间常用的两个计算操作是点乘和叉乘。
两个向量点乘可以得到一个标量。 \[ \vec{a} \cdot \vec{b} = ||\vec{a}|| \ ||\vec{b}|| \cos{\theta} \] 在图形学中,向量叉乘可以在这些方面为我们提供帮助:
- 快速得到两个向量点夹角
- 计算一个向量到另一个向量到投影
- 判断两个方向是否接近
- 提供前后的信息,判断两个向量是处于相同方向还是相反方向。
两个向量叉乘可以得到另一个向量。叉乘得到的向量方向满足右手螺旋定则,并且向量的大小满足如下等式: \[ ||\vec{a} \times \vec{b}|| = ||\vec{a}|| \ ||\vec{b}|| \sin{\theta} \] 利用叉乘,我们可以建立三维中的直角坐标系,即有 \(\vec{x}\times \vec{y} = + \vec{z}\)。如果我们在坐标系中表示两个向量,即\(\vec{a} = (x_a, y_a, z_a)^T, \vec{b} = (x_b, y_b, z_b)^T\),那么叉乘的计算可以表示为: \[ \vec{a} \times \vec{b} = \begin{pmatrix} y_az_b - y_bz_a\\ z_ax_b - x_az_b\\ x_ay_b - y_ax_b\\ \end{pmatrix} \] 实际上,叉乘的计算可以表示为一个伴随矩阵和一个向量相乘的结果,这种形式实际上非常适合计算机的处理。 \[ \vec{a} \times \vec{b} = A^* \vec{b} = \begin{pmatrix} 0 & -z_a & y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0 \\ \end{pmatrix} \begin{pmatrix} x_b \\ y_b \\ z_b \\ \end{pmatrix} \] 此外,叉乘可以用来帮助我们判断两个向量的左右关系,内外关系等。举例来说,\(\vec{a}, \vec{b}, \vec{c}\)三个向量首尾相连构成一个三角形,我们需要判断一个点是否在这个三角形的内侧,只需要判断这个点在三条边的同侧即可。
矩阵Matrix
从几何上理解,我们可以将矩阵看成是一种变换,这里不再进行详细说明,后续也会持续使用到这种思想。
变换Transformation
2D变换
在变换中,我们通常考虑的有缩放,旋转和平移,这三个操作可以组成所有常见的操作。我们提到,矩阵可以看作是一种变换,因此有如下分析:
缩放矩阵:可以实现均匀缩放,不均匀缩放,镜像缩放,切变等操作。考虑缩放前后基坐标\(\vec{i},\vec{j}\)前后的坐标变换,得到缩放矩阵。 \[ \mathbf{S}(s_x, s_y) = \begin{pmatrix} s_x & 0\\ 0 & s_y \\ \end{pmatrix} \] 旋转矩阵:在默认情况下,旋转指的都是按照原点,沿逆时针方向进行旋转。假设旋转角为\(\theta\),则有: \[ \mathbf{R}_{\theta} = \begin{bmatrix} \cos{\theta} & -\sin{\theta}\\ \sin{\theta} & \cos{\theta} \end{bmatrix} \]
对于旋转矩阵来说,通过代入\(-\theta\)可以得到,可以得到\(\mathbf{R}_{-\theta} = \mathbf{R}_{\theta}^T\);同时根据定义,可以得到\(\mathbf{R}_{-\theta} = \mathbf{R}_{\theta}^{-1}\),因此有\(\mathbf{R}_{\theta}^T = \mathbf{R}_{\theta}^{-1}\)。
在数学上,如果一个矩阵的转置等于这个矩阵的逆,那么称这个矩阵为正交矩阵。所以旋转矩阵实际上都是正交矩阵。
对于平移操作,坐标变换可以表示为: \[ \begin{aligned} x' = x + t_x \\ y' = y + t_y \end{aligned} \]
齐次坐标
通过上面的分析我们可以发现,对于缩放和旋转,我们可以将其写作线性变换的形式,\(x^{'}= Mx\),即将变换写成矩阵和向量的乘法形式。但是平移变换无法写作这种形式。因此,为了统一变换的表达形式,引入齐次坐标。在齐次坐标的表示下,我们将2D的点和向量表示成下面的形式: \[ \begin{aligned} \text{2D Point: } (x, y, 1)^T\\ \text{2D Vector: } (x, y, 0)^T\\ \end{aligned} \]
这里关于1和0的理解,一种说法是向量具有平移不变性,0可以保证不破坏这种性质。同时,这种定义也可以满足如下性质:
- v + v = v
- p - p = v
- p + v = p (一个点沿着一个向量移动,得到一个新的点)
- p + p = ? (New point)
在齐次坐标的表示下,第三个位置上的数值不为0或者1的话,则有它表示一个point,并且具有如下的定义: \[ \begin{pmatrix} x \\ y \\ w \end{pmatrix} = \begin{pmatrix} x / w \\ y / w\\ 1 \end{pmatrix} \] 引入齐次坐标之后,我们可以重新对变换的表示进行分析。在齐次坐标下,三种变换的方式得以统一。
缩放矩阵: \[ \mathbf{S}(s_x, s_y) = \begin{pmatrix} s_x & 0 & 0\\ 0 & s_y & 0\\ 0 & 0 & 1\\ \end{pmatrix} \] 旋转矩阵: \[ \mathbf{R}(\theta) = \begin{pmatrix} \cos{\theta} & -\sin{\theta} & 0\\ \sin{\theta} & \cos{\theta} & 0\\ 0 & 0 & 1\\ \end{pmatrix} \] 平移矩阵: \[ \mathbf{T}(t_x, t_y) = \begin{pmatrix} 1 & 0 & t_x\\ 0 & 1 & t_y\\ 0 & 0 & 1\\ \end{pmatrix} \]
tradeoff:英文翻译为权衡,即带来了方便,可能会引入其他问题。一个通俗的表达则是:那么代价是什么呢?
引入齐次坐标,我们统一了变换的表示,但是在其他方面会带来一定的影响。
至此,使用齐次坐标,我们可以将所有的缩放,旋转和平移变换都用一种统一的形式来进行表示。而在2D中的任意一种复杂变换,都可以分解成为这三种变换的组合。我们又知道变换之间的连续作用可以看作是矩阵的连乘,最终的效果相当于一个矩阵作用。也就是说,2D上任意一种复杂变换都可以使用一个齐次坐标矩阵来表示。
3D变换
3D的变换可以从2D进行推广。同样考虑齐次坐标,有如下表示方式: \[ \begin{aligned} \text{3D Point: } (x, y, z, 1)^T\\ \text{3D Vector: } (x, y, z, 0)^T \end{aligned} \] 同样,有推广的3D point表示: \[ \begin{pmatrix} x \\ y \\ z \\ w \end{pmatrix} = \begin{pmatrix} x / w \\ y / w\\ z / w \\ 1 \end{pmatrix} \] 对应在3D空间中,缩放,旋转和平移同样可以统一为一个变换矩阵,且这个变换矩阵的维度为\(4 \times 4\)。
缩放矩阵: \[ \mathbf{S}(s_x, s_y, s_z) = \begin{pmatrix} s_x & 0 & 0 & 0\\ 0 & s_y & 0 & 0\\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1\\ \end{pmatrix} \] 旋转矩阵:
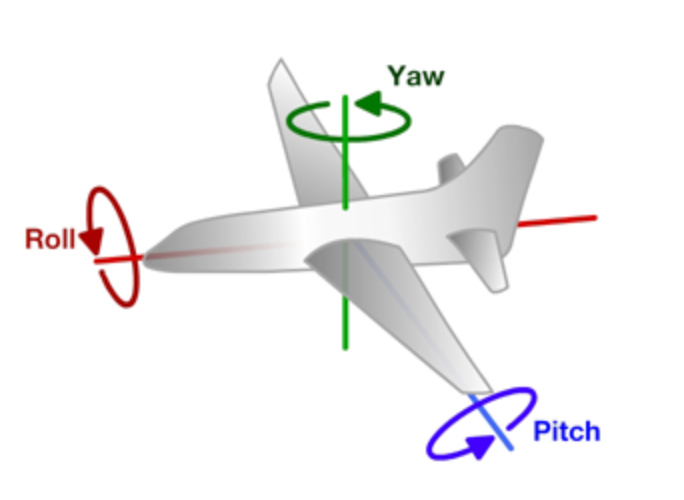
3D中的旋转相比2D中会复杂一些,一个任意的旋转可以分解为绕x、y、z轴的旋转,而这些旋转矩阵有相对简单的旋转矩阵 \[ \begin{aligned} \mathbf{R}_x(\theta) = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & \cos{\theta} & -\sin{\theta} & 0\\ 0 & \sin{\theta} & \cos{\theta} & 0\\ 0 & 0 & 0 & 1\\ \end{pmatrix} \\ \mathbf{R}_y(\theta) = \begin{pmatrix} \cos{\theta} & 0 & \sin{\theta} & 0\\ 0 & 1 & 0 & 0\\ -\sin{\theta} & 0 & \cos{\theta} & 0\\ 0 & 0 & 0 & 1\\ \end{pmatrix} \\ \mathbf{R}_z(\theta) = \begin{pmatrix} \cos{\theta} & -\sin{\theta} & 0 & 0\\ \sin{\theta} & \cos{\theta} & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{pmatrix} \end{aligned} \] 任意的旋转可以分解为绕x、y、z轴的旋转,其中旋转的角度通常被称为roll、pitch和yaw。可以参考下面的图,其中沿机身方向为X轴,沿机翼方向为Y轴,垂直机身方向为Z轴。
除了基本的旋转矩阵之外,还有一个罗德里格斯旋转公式。它描述了绕任意轴\(\mathbf{n}\),旋转任意角度\(\alpha\)的公式求解: \[ \mathbf{R}(\mathbf{n} ,\alpha) = \cos{(\alpha)} \mathbf{I} + (1-\cos{(\alpha)}) \mathbf{n}\mathbf{n}^T + \sin{(\alpha)} \begin{pmatrix} 0 & -n_z & n_y\\ n_z & 0 & -n_z\\ -n_y & n_x & 0\\ \end{pmatrix} \] 平移矩阵: \[ \mathbf{T}(t_x, t_y, t_z) = \begin{pmatrix} 1 & 0 & 0 & t_x\\ 0 & 1 & 0 & t_y\\ 0 & 0 & 1 & t_z\\ 0 & 0 & 0 & 1\\ \end{pmatrix} \]
Viewing Transformation
计算机需要显示3D物体,具体来说需要将3D空间中的坐标转化为图像空间中的像素坐标。在实际操作中,整个过程分为两部分,第一部分是将3D空间的坐标进行一定的处理,使得要处理的场景都处于标准立方体中;第二部分是从标准立方体转化到像素坐标。这一节主要介绍的就是第一部分,而完成第二部分的操作包括后续的光栅化、光线追踪等技术。
第一部分的流程主要涉及如下环节(可以类比拍照)也统称为MVP变换:
- model transformation:摆好被拍的东西
- view transformation:摆好照相机
- projection transformation:开始照相
view transformation
model transformation和view transformation两者统一完成的是一种刚体变换,保持相机和场景物体的相对位置不变,同时将相机按照特定的方式固定在原点。(特定的方式指的是相机位置在原点,相机正面朝向在\(-z\))该变换只和摄像机的原始描述向量有关。
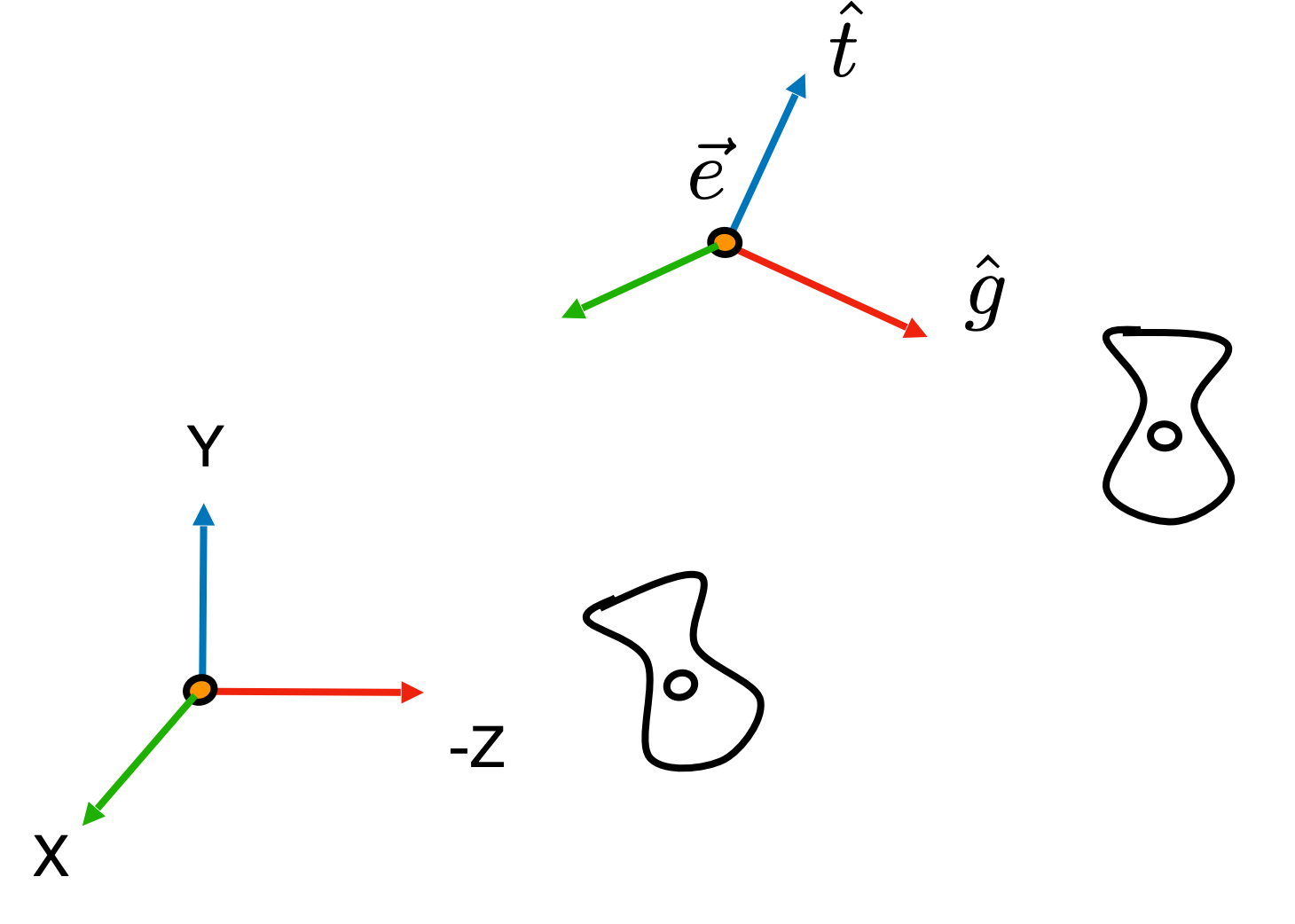
这里的相机通常使用会使用三个向量来定义:
- 指定相机的位置position:\(\vec{e}\)
- 指定相机的正面朝向,即看的方向:\(\vec{g}\)
- 指定相机的向上方向,即怎么拿相机:\(\vec{t}\)
根据定义,其中\(\vec{g}\)和\(\vec{t}\)向量相互垂直。
可以注意到,只要相机和被观察的物体之间的相对位置没有发生改变,那么得到的图像就是一样的。因此在实际进行操作的时候,一般会将相机固定到原点,那么被观测的物体也需要作相同的变换。具体来说,我们会将\(\vec{e}\)移动到原点,\(\vec{t}\)移动到y轴方向,\(\vec{g}\)移动到-z方向。这个过程称为view transformation。
view transformation作为一个变换,同样对应一个变换矩阵,记这个矩阵为\(\mathbf{M}_{view}\)。考虑上面的变换过程,变换可以分为两步:
- 将\(\vec{e}\)移动到原点,对应一个平移变换\(\mathbf{T}_{view}\)
- 将\(\vec{g}\)移动到-z方向,将\(\vec{t}\)移动到y方向,将\(\vec{g} \times \vec{t}\)移动到x方向,对应一个复杂的旋转变换\(\mathbf{R}_{view}\)
以上面的符号标记,我们有\(\mathbf{M}_{view} = \mathbf{R}_{view}\mathbf{T}_{view}\)。其中平移矩阵比较好求,可以直接写出: \[ \mathbf{T}_{view} = \begin{bmatrix} 1 & 0 & 0 & -x_e \\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \end{bmatrix} \] 而对于这个旋转变换,直接写其实并不好写,我们可以先考虑它的逆变换\(\mathbf{R}^{-1}_{view}\),从物理意义上,它表示将x移动到\(\vec{g} \times \vec{t}\),将y移动到\(\vec{t}\),将z移动到\(-\vec{g}\),因此可以得到 \[ \mathbf{R}_{view}^{-1} = \begin{bmatrix} x_{\vec{g} \times \vec{t}} & x_{\vec{t}} & x_{-\vec{g}} & 0\\ y_{\vec{g} \times \vec{t}} & y_{\vec{t}} & y_{-\vec{g}} & 0\\ z_{\vec{g} \times \vec{t}} & z_{\vec{t}} & z_{-\vec{g}} & 0\\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \] 而前面我们提到过,旋转矩阵属于正交矩阵,因此有: \[ \begin{aligned} \mathbf{R}_{view} &= (\mathbf{R}_{view}^{T})^{T} = (\mathbf{R}_{view}^{-1})^{T} \\ &= \begin{bmatrix} x_{\vec{g} \times \vec{t}} & y_{\vec{g} \times \vec{t}} & z_{\vec{g} \times \vec{t}} & 0\\ x_{\vec{t}} & y_{\vec{t}} & z_{\vec{t}} & 0 \\ x_{-\vec{g}} & y_{-\vec{g}} & z_{-\vec{g}} & 0 \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \end{aligned} \]
projection transformation
完成了相机变换即view transformation之后,我们就可以进行投影projection了。projection完投影主要分为两大类,分别是正交投影和透视投影,透视投影会形成近大远小的效果,而正交投影则相当于相机距离无限远。
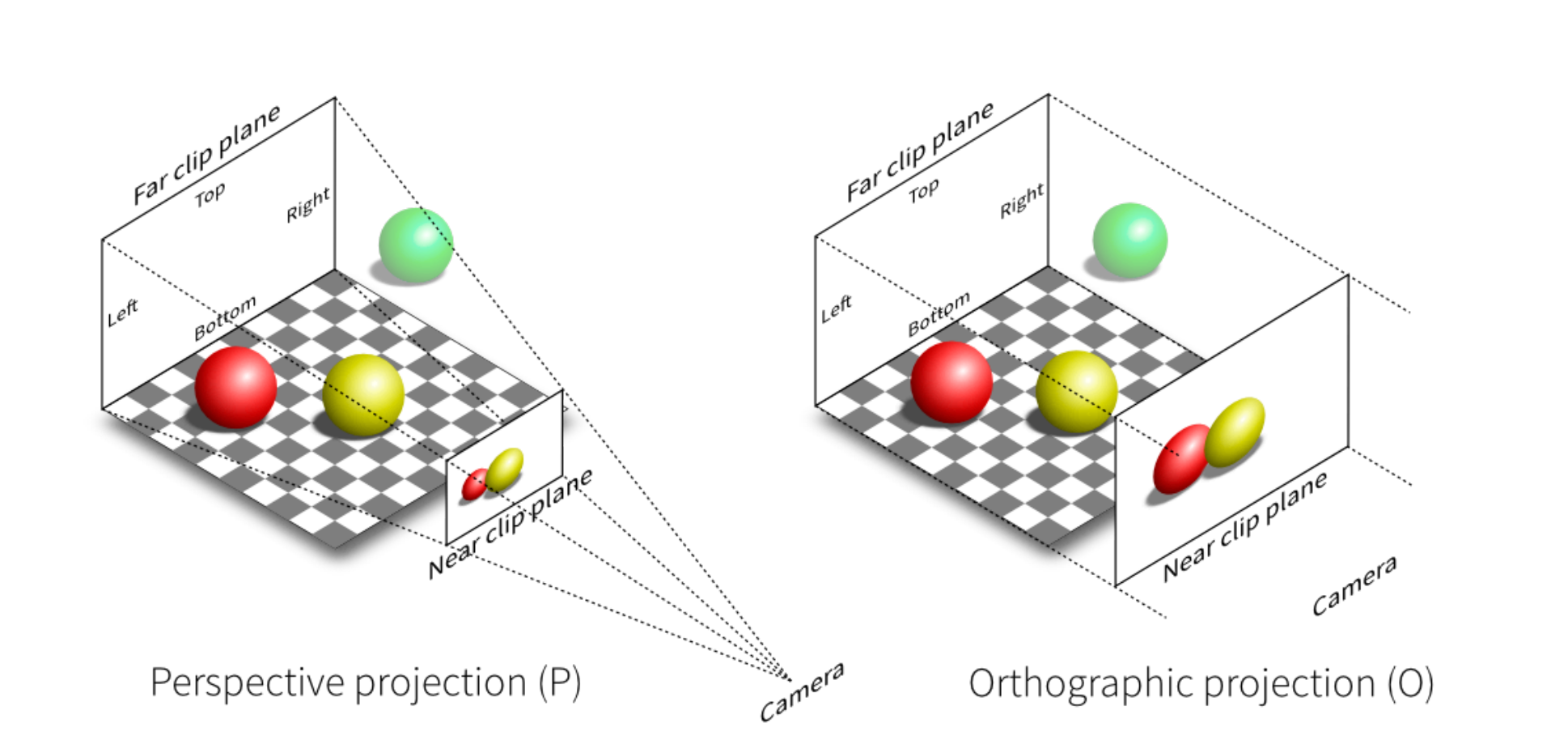
正交投影
正交投影(Orthographic Projection)。正交投影有一个非常简单的方式,就是直接消除z轴坐标,将物体坐标直接映射到平面上,当然需要根据深度信息考虑遮挡关系。不过实际上,在进行正交投影的时候,通常会约定将结果拉到标准(canonical)立方体中,即\([-1, 1]^3\)范围内。(这种约定的方式会在后续的工作中给我们带来方便)
考虑空间中的一个立方体,对它进行正交投影,需要经过平移和缩放:
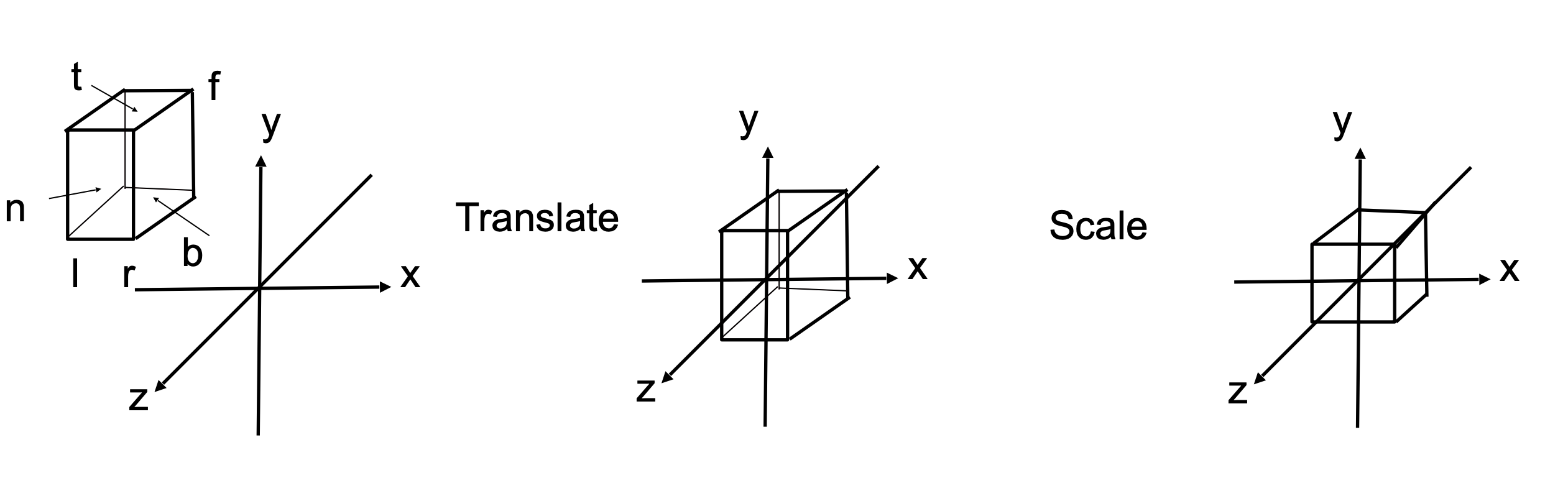
可以得到投影变换矩阵为: \[ \mathbf{M}_{ortho} = \mathbf{S}\mathbf{T}=\begin{bmatrix} \frac{2}{r-l}&0&0&0\\ 0&\frac{2}{t-b}&0&0\\ 0&0&\frac{2}{n-f}&0\\ 0&0&0&1\\ \end{bmatrix}\begin{bmatrix} 1&0&0&-\frac{r+l}{2}\\ 0&1&0&-\frac{t+b}{2}\\ 0&0&1&-\frac{n+f}{2}\\ 0&0&0&1\\ \end{bmatrix} \]
透视投影
透视投影(Perspective Projection)的完成,可以看作两个步骤的合成,先将锥形压缩成长方体,然后再对这个长方体进行正交投影。
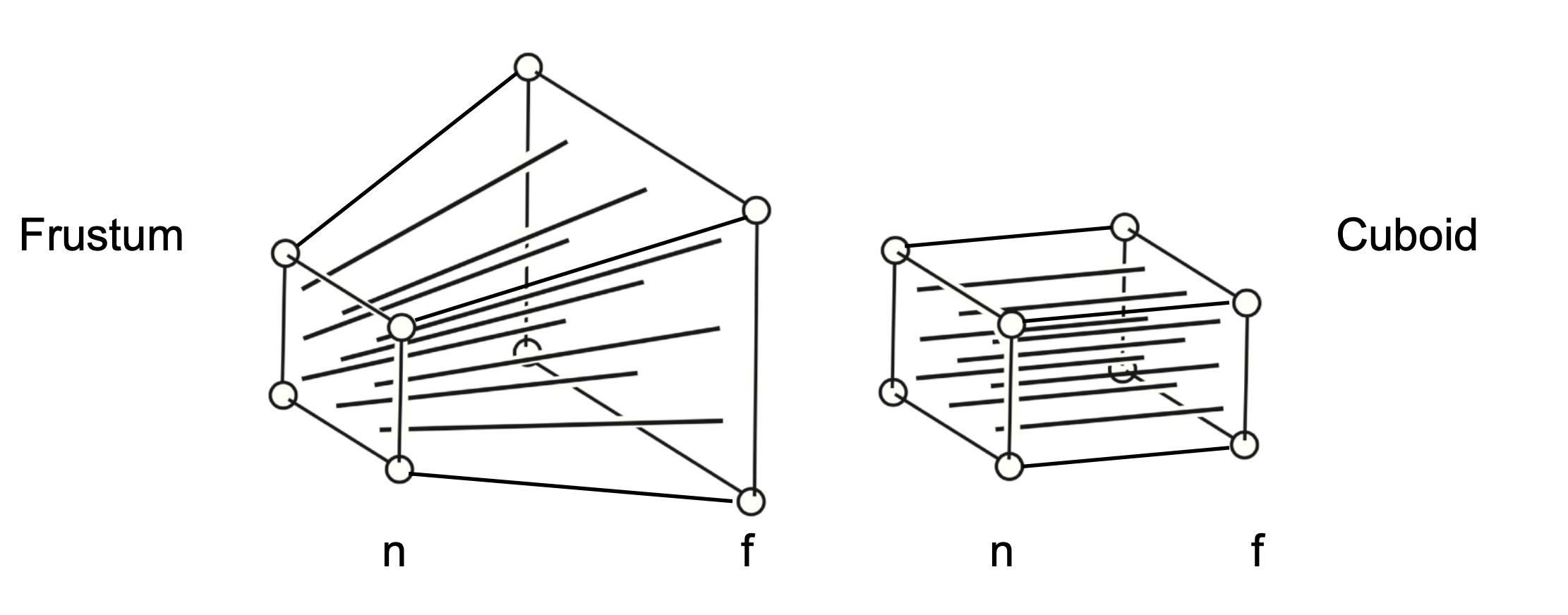
其中这个锥形表示视锥,视锥的表示可以如图所示,其中包括视点,近平面和远平面:
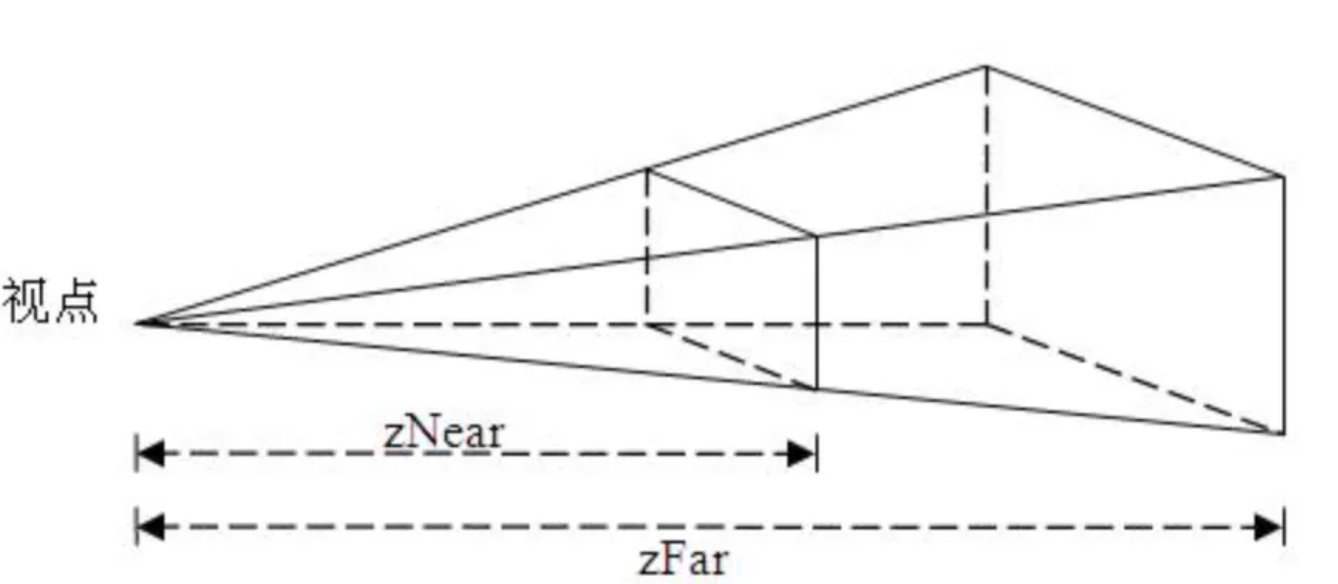
视锥中有几个比较重要的参数:
- 视点的位置
- 近平面和远平面,即zNear和zFar
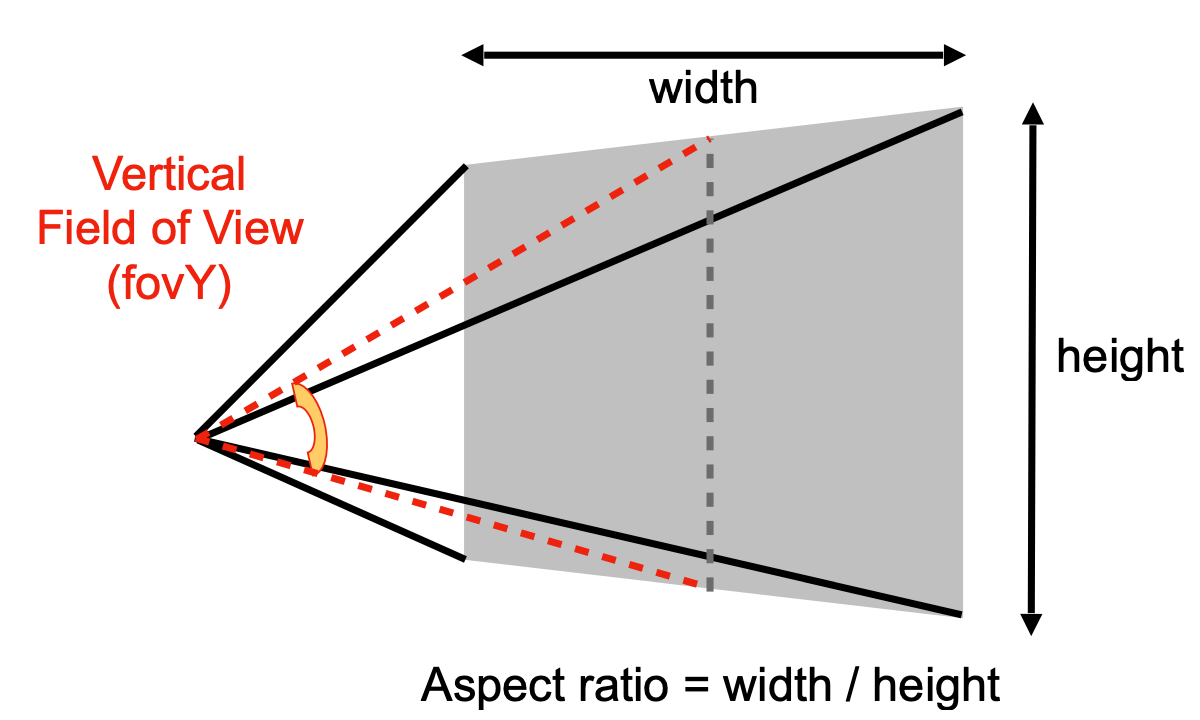
- 实际窗口的宽高比(aspect ratio),即width/height
- 视角范围,使用角度来描述,即图中的Vertical Field of View。这里的定义是使用了宽的中点,实际上根据宽高比,我们可以很容易计算出使用高的中点时,对应的可视角度是多少
将透视投影使用矩阵表示,则有\(\mathbf{M}_{persp} = \mathbf{M}_{ortho}\mathbf{M}_{persp \rightarrow ortho}\),其中\(\mathbf{M}_{ortho}\)就是上面得到的正交投影变换矩阵,\(\mathbf{M}_{persp \rightarrow ortho}\)则有如下定义(推导过程省略) \[ \mathbf{M}_{persp \rightarrow ortho} = \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \]