Games101(4)-光线追踪
Ray Tracing光追
背景引入
通过光栅化Rasterization,我们已经可以将3D空间中的物体渲染在屏幕上,但是它仍旧存在一些缺点。例如,光栅化不能很好地处理全局的影响,例如无法处理软阴影(Soft Shadows)、Glossy Reflection、间接光照(光线经过多次弹射)等。虽然光栅化能够做得比较快,但是它在过程中存在多处近似,使得得出的结果仍然是不真实的。
光线追踪Ray Tracing是另一种渲染方式,同样能够将3D空间中的物体渲染在屏幕上。与光栅化不同的是,光追的处理过程更加贴近真实的情况,能够得到非常真实的结果。当然相对的,光追的速度非常慢(trade off!)。当然现在也有一些研究方向是实时光追。
Tips:下面是从另一种角度来对比光栅化和光追。
计算机图形学的基本任务就是将在3D世界中的几何物体以某种特定的视角,在2D平面上以像素的形式渲染出来。
一般来说,渲染可以分为两种思路(两种思路有点类似于双重循环的不同循环顺序):
- object-order rendering:每个object会逐个考虑,在考虑每一个object的过程中,判断哪些像素被它影响并进行更新。
- image-order rendering:每个pixel会逐个考虑,在考虑每一个pixel的过程中,判断共有哪些物体影响这个像素,并计算这个像素最终的值。
object-order rendering在速度和效率上有着很大的优势。相比于反复检索被着色像素需要的场景物体,场景中每个物体只需遍历一遍的方法显然快很多。光栅化使用的就是object-order rendering思路。
image-order rendering会更加简单粗暴,也更加灵活,只不过需要更大的计算量,但是效果也往往比较好。光追使用的就是image-order rendering思路。
基础 Ray Tracing
在介绍光追算法之前,我们可以先对光线进行一些简单的定义和说明。我们认为光线沿直线传播、不同光线之间不会发生碰撞、光线从光源发出,最后到达眼睛。似乎上面都是一些很普通的定义,的确也正是这样。考虑摄像机/人眼能够看见物体(成像),是因为光线在物体上弹射之后进入摄像机/人眼中。而光线追踪实际上利用了光路的可逆性,它考虑的是光线从摄像机/人眼出发,在物体之间弹射,最后到达光源。这也是光追的核心思想。
首先考虑基础的光追算法(Basic Ray Tracing Algorithm),也称为光线投射(Ray Casting)。该算法假设:
- 人眼是针孔摄像机(one point),光源是点光源
- 光线打到场景中的物体会发生完美的反射/折射
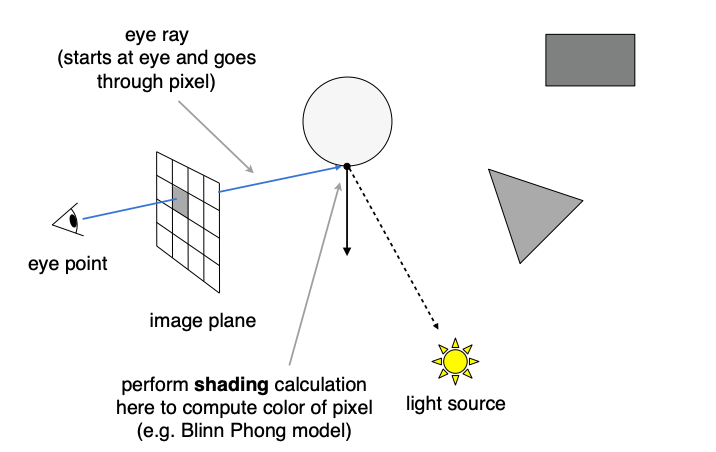
基础Ray Tracing分为两部分,第一部分是从人眼向每个图像中的每个像素投射光线,第二部分是检测是否处在阴影当中。
- 从眼睛开始,向成像屏幕的每个像素投射光线,光线(Eye Ray)会打到最近的一个物体上(实际上“最近的”简单地就解决了深度测试的问题),得到一个交点
- 从这个交点与光源之间可以连接一条光线(Shadow Ray),如果这条线上没有东西遮挡,就认为这点可以被光线照亮,此时就可以使用各种Shading模型得到像素的值(例如在光栅化中提到的Blinn-Phong着色模型);如果这条线上有东西遮挡,就认为该点在阴影当中
Whitted-Style Ray Tracing
介绍
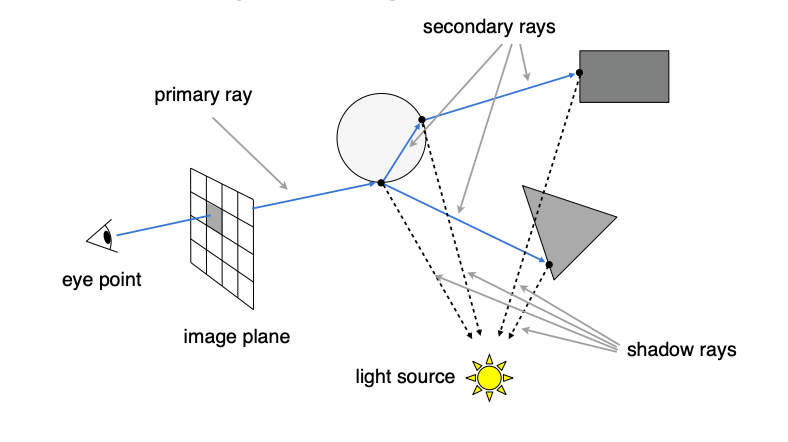
注意到,在基础Ray Tracing中,光线只进行一次弹射,仍然不是很符合实际。于是引出下面的方法,即Whitted-Style Ray Tracing。
Whitted-Style Ray Tracing在Basic Ray Tracing的基础上,考虑投射的光线可以继续传播,打到场景中的其他物体上,即光线的多次弹射。在每一个交点上,我们都可以计算一次着色,最终的该像素的总体着色值是所有弹射点的着色值总和。(需要考虑到光线在弹射的过程中有能量损失,最终并不会出现类似过曝的现象)。
光线与平面求交
whitted-Style Ray Tracing的思想其实比较好理解,但是在实际实现过程中,会涉及到许多技术相关的问题。接下来就进行介绍。
首先遇到的第一个问题就是如何计算光线与表面的交点,为此首先需要对光线进行数学上的定义,考虑光线是一个射线,从某个点\(\mathbf{o}\)出发,沿着方向\(\mathbf{d}\)进行传播,因此可以得到光线方程: \[ \mathbf{r}(t) = \mathbf{o} + t \mathbf{d}, \quad 0 \le t < +\infty \] 定义了光线方程之后,就可以求光线与表面的交点了。如果物体的表面可以通过某种方程来显示描述,那么就可以通过联立方程组来计算出交点。当然这种方式推广到隐式表示中也是成立的,只要物体的表面可以通过某种方程来描述,就可以通过联立方程组的方式来求出交点。
如何解方程组不在这里考虑,我们只需要知道实际上有很多数值计算的方式来解方程组。
当然还有一种常见的方式是利用众多三角形面来表征物体的表面,也就是需要处理光线和三角形mesh的交点。我们可以将每个三角形看作是一个平面,对每个三角形,求出光线与该平面的交点,然后判断该交点是否在三角形内部即可。
由于我们知道三角形的法线,同时也知道三角形的三个顶点坐标,因此可以很容易写出平面方程(平面上的任意向量都会垂直于法线)。通过联立方程可以算出光线与平面的交点,再通过判断该点是否在三角形内部即可完成对于一个三角形的操作。
上面的方式对于一个三角形需要执行两步,实际上我们可以利用重心坐标来一步计算出是否有满足条件的交点。考虑三角形的三个顶点分别为\(\mathbf{p_0},\mathbf{p_1}, \mathbf{p_2}\),那么光线与三角形内部相交的情况就会满足下面的式子,其中等式的左边是光线方程,右边是用重心坐标表示的三角形内部的任意点. \[ \mathbf{o} + t \mathbf{d} = (1 - b_1 - b_2)\mathbf{p_0}+b_1\mathbf{p_1} + b_2\mathbf{p_2},\quad \text{其中} t > 0,1-b_1-b_2 \ge 0, b_1 \ge 0, b_2 \ge 0 \] 我们需要求解的就是满足条件的三个未知量\(t,b_1,b_2\)。该方程的求解可以通过克莱姆法则完成。
实际上,上面说的算法的名称为Möller–Trumbore intersection algorithm
AABB加速
通过上面描述的光线与三角形求交的方式,我们实际上已经可以利用光追算法来渲染出图像,但是过程中会存在性能问题。考虑处理的像素有pixels个,场景中的三角形有traingles个,光线弹射的次数为bounces,那么所需计算的次数就是\(pixels \times traingles \times bounces\)。实际上场景中的物体所含有的全部三角形数目是非常巨大的,导致这种方式的计算次数也会变得非常巨大,这种性能是无法被接受的。为此,需要对计算方式进行一定的优化。
每个物体由众多三角形面构成,每次计算需要考虑光线是否与物体相交。可以观察到,如果遍历场景中的所有三角形,有很多遍历是无意义的。考虑某个物体的包围盒(Bounding Box),一种加速思想是,如果光线与包围盒没有交点,那么肯定与这个物体没有交点,那么这个物体所包含的三角形就可以全部不用考虑了。并且注意到与物体求交是困难的,与包围盒求交是简单的,这种方式可以大大地简化计算。
一个物体的包围盒有很多,我们常用的是一种称为轴对齐包围盒的Bounding Box,对应的英文名称为Axis-Aligned Bounding Box,简称AABB。AABB是一个矩形,其中的每个面都会平行于x,y,z轴构成的其中一个平面。这样处理的好处是得到了一个表示简单的Bounding Box,计算光线与它是否相交也会变得很简单。
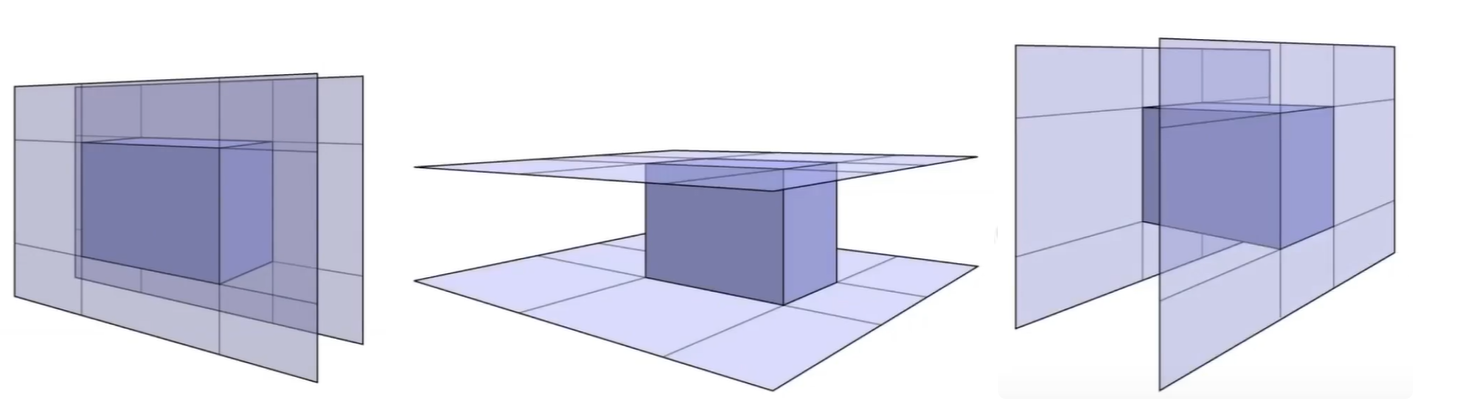
那么光线如何与AABB求交?我们将AABB考虑为三个对面(\(3\times2=6\) 一共六个面),当光线进入了三个对面,才算进入了包围盒;当光线离开了任何一个对面,就算离开了包围盒。因此我们可以计算光线进入x,y,z三组平面的\(t_{min},t_{max}\)(即求光线与平面的交点,此时的平面较为特殊,是平行于坐标系平面的平面,因此计算起来也会比较简单),那么光线进入包围盒的时间\(t_{enter}\)就是所有\(t_{min}\)的最大值,离开包围盒的时间\(t_{exit}\)就是所有\(t_{max}\)的最小值。
- 如果\(t_{exit} < 0\),表示包围盒在光线的后面(射线的后面),那么不可能有交点
- 如果\(t_{enter} < 0, t_{exit} > 0\),表示光线在包围盒中,那么一定有交点
- 如果\(t_{enter} > 0, t_{exit} >0\),那么只有当\(t_{enter} < t_{exit}\),即光线在包围盒中存在了一定时间,才与包围盒有交点
综上所述,只有当\(t_{enter} < t_{exit}\) 且 \(t_{exit} >0\) 时,光线与包围盒有交点。
加速结构
AABB提供了一种思想,即利用包围盒来加速Ray Tracing。而在实际应用的过程中,有多种使用方式,具体差别在于如何划分场景中的AABB。接下来所说的划分结构,或者称为加速结构 都是在执行光追之前进行构建的,用以加速光追的执行。
一种最为简单的方式是将场景进行均匀划分(uniform grid),得到众多大小相等的小格子。这些小格子可以被分为两类,一类是与物体表面相交的格子,另一类是没有与任何物体相交的格子。与物体相交的格子会存储所有与之相交的物体(的所有三角形)。当光线投射的时候,我们可以先判断光线与哪些格子相交,在这些格子中,进一步判断该格子中是否有物体,如果有,就对其中的物体三角形进行遍历处理,进一步判断光线是否与物体相交。
均匀划分实现简单,但是划分数目会很大程度上影响性能。如果格子太少太稀疏,那么无法起到加速作用;如果格子太多太密集,则需要多次判断光线是否与格子有交点,可能也会降低效率。
一个经验上的做法是划分出\(C \times \text{num of objects}\)个数的格子,其中\(C=27\)。
均匀划分在一些情况下的确能够起到加速作用,但是它不适用于场景中物体分布不均匀的情况,即场景中某个地方有大量的物体,某个地方又有大量的空白。基于此,我们又提出了一些不均匀的空间划分结构,不均匀的空间划分主要希望使得在空白的地方格子大些,在物体密集的地方格子小一些。常见的空间划分结构包括Oct-Tree、KD-Tree和BSP-Tree。
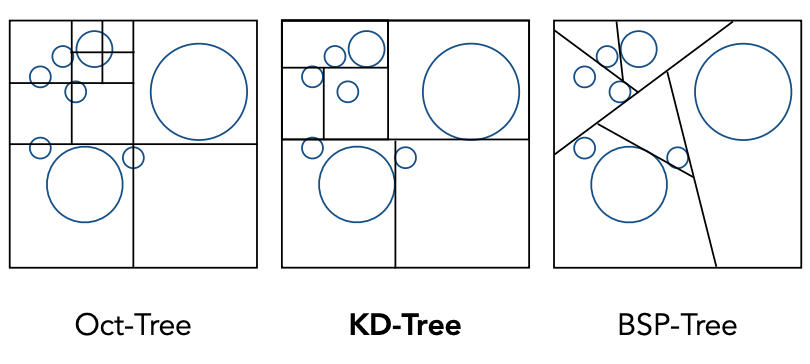
Oct-Tree(八叉树)按照每次八分的方式对场景进行递归划分(三次切分,上下左右前后),每次划分后可以得到新的八个子grid,在每个节点都递归地进行划分,划分停止的条件是发现该grid中没有物体或者该grid中的物体数量足够少。
八叉树的划分方式与维度有关,随着维度的上升,划分出的空间数量会呈指数增长。为了解决这个问题,出现了KD-Tree的方法。对于每个grid,KD-Tree采取的方式是只进行一次划分,并且这次划分是沿着某个轴进行的,并且按照xyzxyz的方式按序改变沿着的轴。最终形成的树是一个二叉树,中间节点只存储了指向子空间的指针,在叶子结点中存放了对应空间中所有物体或者所有三角形面的信息。
BSP-Tree的划分方式与KD-Tree基本一致,不同之处在于BSP-Tree的划分不一定是沿着固定的某个轴,而是可以任意划分。划分方向不规则也就导致了求交不好计算,随着维度升高也会变得越来越复杂。
上面所说的划分方式都是对空间进行划分,可能会出现同一个物体被多个grid都存储的情况。另一种思想是基于物体进行划分,称为Bounding Volume Hierarchy(BVH)。对于每个包围盒,可以其中的物体划分为两部分,对于每部分的物体可以重新计算出一个包围盒,递归地进行该操作,直到某个包围盒中的三角形面数小于某个设定的值。对于BVH来说,它的包围盒之间可能出现重叠,但是一个物体只会出现在一个包围盒当中。BVH划分的是物体,具体的划分方式也有多种,例如为了让空间均匀分布,每次将最长的轴切断,沿着该轴找到中间的三角形,以它为分界线进行划分。
辐射度量学Radiometry
在Whitted-Style Ray Tracing算法作用下,能够得到一定效果的成像结果,但是真实性仍然较为缺乏,这是因为我们所使用的光线作用方式仍然是简化的,近似的。因此,为了达到更好的效果,我们需要定义更加精确的光线作用方式,因此首先引入辐射度量学Radiometry。辐射度量学精确地定义了与光相关的一系列物理量和方法,来描述光如何与表面发生作用。
光照描述
- Radiant Energy:光线辐射出来的能量\(Q\),单位为焦耳\(J\)
- Radiant Flux:光线单位时间内辐射的能量\(\Phi\),类似于功率,单位为瓦特\(W\);不过更常用的单位是流明\(lm\)
\[ \Phi = \frac{d Q}{ d t} \]
注意,在图形学中描述的能量通常都是单位时间的能量,即这里的flux。
- Radiant Intensity:单位立体角上的Flux,单位为\(cd(candela)\)
\[ I(\omega) = \frac{d \Phi}{d \omega} \]
这里涉及到一个立体角的概念。在平面上,角的定义我们非常熟悉,即弧长/半径,而立体角就是角度在三维空间中的衍生。考虑空间中的一个球,一个立体角会对应球面上的一个面积,那么立体角就等于 球面面积/半径的平方。一个平面的圆形,它的角度是\(2\pi\);一个空间中的球形,它的立体角是\(4\pi\)。

考虑在半径为\(r\)的球中,一条具体半径的确定可以通过\((\theta,\phi)\)来确定,单位立体角则考虑在这两个方向上旋转一个非常小的角度,然后计算对应的立体角。可以看到单位立体角与具体的半径方向有关,即与对应方向\(\omega\)有关。最终得到结论: \[ d\omega = \sin{\theta} d\theta d\phi \]
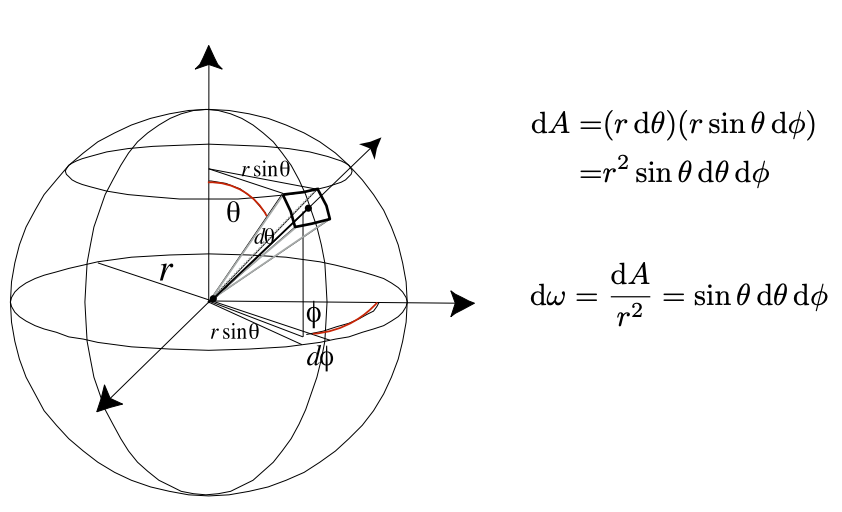
- Irradiance:单位面积上的flux通量,即考虑垂直于光线的面积,单位为\(lux\)
\[ E(\mathbf{x}) = \frac{d \Phi(\mathbf{x})}{d A} \]
- Radiance:光线在单位面积\(A\),单位立体角\(\omega\)上辐射出的Flux。这个概念也是描述环境中光的分布的基本概念。
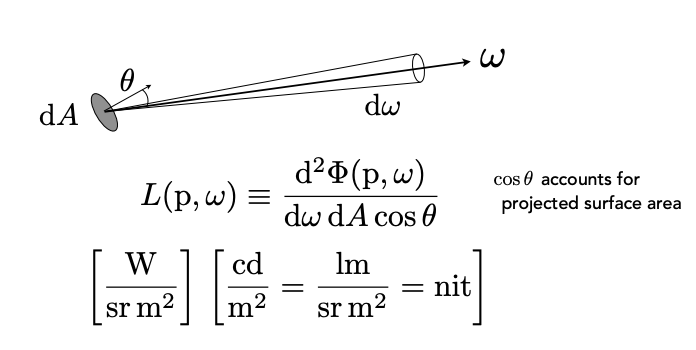
Radiance可以分为入射和出射的情况,这两种情况可以从不同角度进行理解。
- 对于入射Radiance,可以理解为从每个单位立体角上到达dA的光线的能量,即:
\[ L(\mathbf{p}, \omega) = \frac{dE(\mathbf{p})}{d\omega \cos{\theta}} \]
- 对于出射Radiance,可以理解为从每个单位投影面积上辐射出的能量,即:
\[ L(\mathbf{p}, \omega) = \frac{dI(\mathbf{p}, \omega)}{dA \cos{\theta}} \]
相比于Irradiance,Radiance增加了方向性。Irradiance描述了单位面积上接收/辐射的能量,Radiance描述的则是单位面积上对某个方向接收/辐射的能量。对Radiance沿着球面进行积分,就可以得到Irradiance。
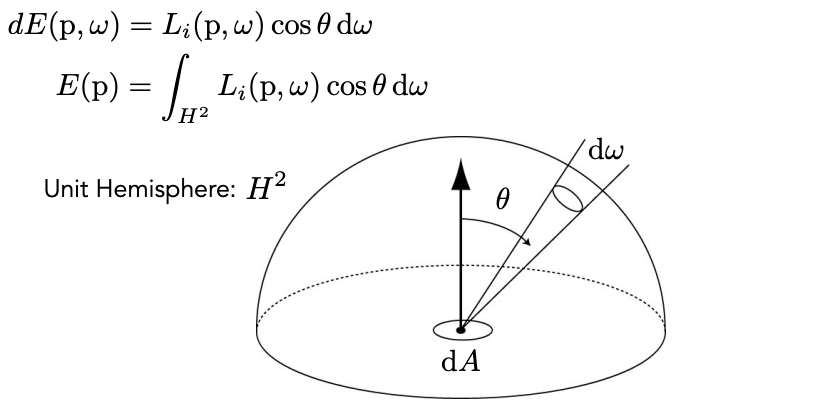
BRDF双向反射分布函数
在定义了上面的物理量之后,我们就可以对光线作用进行描述。BRDF,全称为Bidirectional Reflectance Distribution Function,双向反射分布函数,就描述了光线与物体如何进行作用。
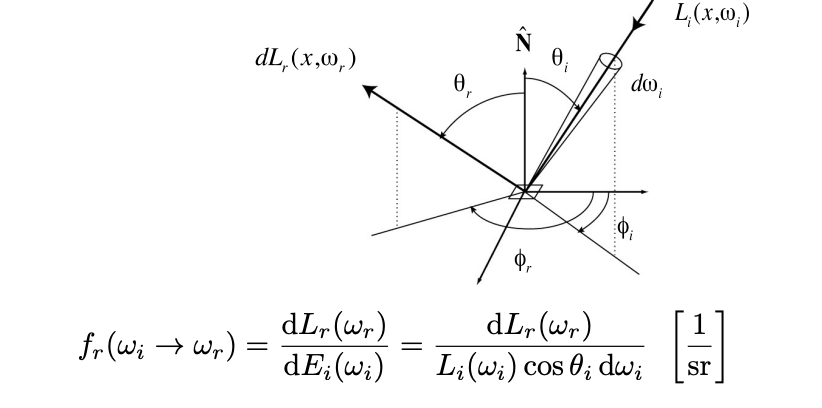
考虑在某个点point上发生的光线反射,从某个方向\(\omega_i\)来的Radiance会转化为dA吸收的能量E,这份能量会转化为向其他方向\(\omega_r\)出射的Radiance。
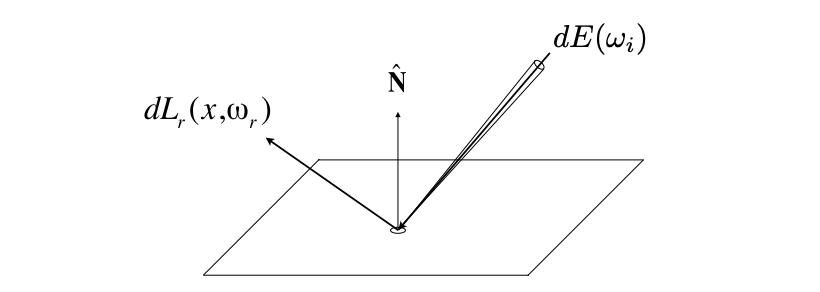
- 入射Radiance:\(dE(\omega_i) = L(\omega_i)\cos{\theta} d\omega_i\)
- 出射Raidance:\(dL_r(\omega_r)\)
而BRDF就是一个函数,用来描述在这个点上,如何将自己吸收到的能量分配到其他各个方向上去。
渲染方程
通过BRDF,我们可以知道每个入射光最后反射出去的Radiance。那么将所有入射方向上光的贡献都进行累计,然后计算对某个特定出射方向的贡献,既可以得到反射方程。
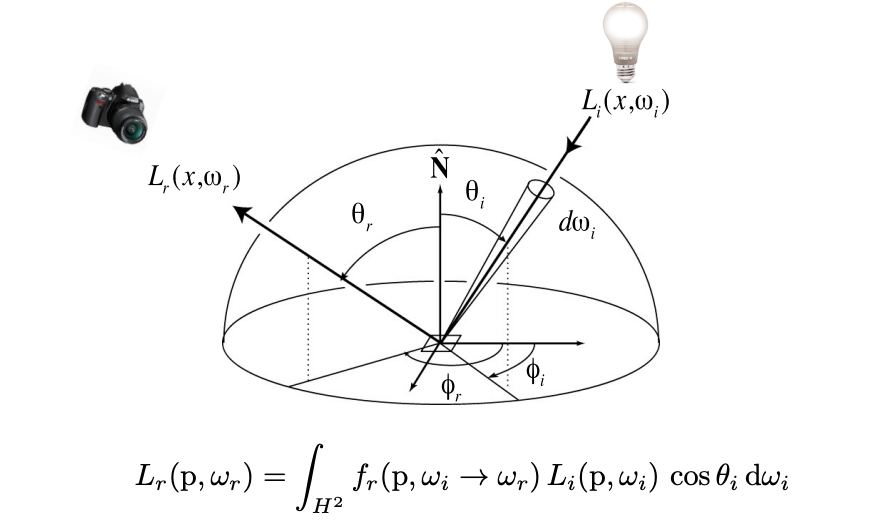
在反射方程中,\(L_i(p,\omega_i)\cos{\theta_i}d\omega_i\)表示来自某个方向上的入射光,乘上一个BRDF,得到该入射光对于特定出射方向的贡献。
但是需要注意的是,这里的入射光除了来自光源,还可能来自其他物体反射的光,而其他物体反射的光也需要利用反射方程来计算,这就是一个递归情况。
为了使得适用情况更加广泛,这里将反射方程扩展为渲染方程,实际上就是考虑物体自己也会发光,增加一项发光项。 \[ L_o(p, \omega_r) = L_e(p, \omega_o) + \int_{\Omega+} L_i(p,\omega_i)f_r(p, w_i, w_r)(n\cdot\omega_i)d\omega_i \] 更进一步对渲染方程进行分析:
- 如果是一个点光源或者多个点光源,则可以使用累加;
- 如果是面光源,则相当于一堆点光源的集合;
- 如果入射光是其他物体反射而来,则将物体当成面光源,对立体角进行积分
从渲染方程出发,最后经过推到可以得到下面的表达: \[ L = E + KE + K^2E + K^3E + ... \] 其中L是最终需要得到的结果,E是本身发出的能量,K是反射因子。
这个式子告诉我们,最终得到的结果可以分解为光线弹射从0到无数次的结果:
- 光线弹射0次:直接打到眼睛中,即我们看到的光源
- 光线弹射1次:光线从光源出发,打到物体经过一次弹射后进入眼睛,即直接光照
- 光线弹射2次:光线从光源出发,打到物体经过两次弹射后进入眼睛,光线弹射两次以上都属于间接光照
- ...
最终全局光照=光源+直接光照+间接光照。
从这个角度进行考虑,光栅化只能告诉我们光线弹射0次和1次的光照内容,但是对于后续的间接光照则较难实现。光线弹射次数越多,得到的全局光照效果越趋近于收敛。
路径追踪Path Tracking
通过辐射度量学,我们可以得到渲染方程。渲染方程描述了光线在实际环境中的作用方式,光追实际上就是对这个渲染方程进行求解。接下来将介绍其中一种求解方式,蒙特卡洛路径追踪(Monte Carlo Path Tracing)。
蒙特卡洛积分
首先介绍蒙特卡洛积分。考虑积分,如果我们知道一个函数的解析式,并且该函数的原函数也能够很好地表示出来,那么利用牛顿-莱布尼茨公式就能够很方便地计算积分值。考虑其他一些更加常见的情况,某个函数的解析式并不能够很容易地表达出来,从而原函数也不能容易地给出。对于这类函数,如果我们只关心最终的积分数值而不关心解析式的话,就可以使用蒙特卡洛积分的方式来近似得到这个积分值。
考虑下面这个不规则的函数,需要求它在区间\([a, b]\)的积分值,利用蒙特卡洛积分的方式完成:
- 每次在区间\([a,b]\)之间进行采样,采样得到一个\(x_i\),得到对应的\(f(x_i)\),将该值认为是长方形的高,则得到长方形的面积为\(f(x_i)\times (b-a)\),用这个值近似整个积分的值;
- 重复采样,得到一系列近似结果。最终认为这些近似结果的平均值就是我们需要得到的\(\int_a^bf(x)dx\)的值;
- 这相当于重复采样得到\(f(x_i)\),然后计算出它的平均,再乘上范围\([a, b]\)。

下面可以数学的角度对蒙特卡洛积分进行定义,考虑一个函数\(f(x)\),我们需要求它在某个范围内的积分\(\int_a^bf(x)dx\)。考虑对自变量\(x\)进行抽样,得到一个随机变量\(X_i\)。假设该随机变量服从某个分布,即$X_i p(x) $,那么最终得到的蒙特卡洛积分模拟值为: \[ \int_a^b f(x) dx = \frac{1}{N} \sum_{i=1}^{N} \frac{f(X_i)}{p(X_i)},\quad X_i \sim p(x) \]
路径追踪
我们说光追是对渲染方程进行求解。渲染方程中出现了一项积分项,求解这项积分项就可以通过蒙特卡洛积分来进行。
注意后续的渲染方程都暂且不考虑自身发光项,仅考虑直接光照和间接光照。
观察渲染方程中的积分项: \[ \int_{\Omega+} L_i(p,\omega_i)f_r(p, w_i, w_r)(n\cdot\omega_i)d\omega_i \] 要利用蒙特卡洛积分对齐进行求解,那么需要对\(\omega\)进行采样。例如假设采样遵守半球内的均匀分布,则有\(p(\omega_i) = 1/2\pi\)。利用蒙特卡洛积分求解,则有如下表达式,其中\(pdf(\omega_i)\)表示采样的概率分布。 \[ \begin{aligned} L_o(p, \omega_r) &= \int_{\Omega+} L_i(p,\omega_i)f_r(p, w_i, w_r)(n\cdot\omega_i)d\omega_i \\ &=\frac{1}{N} \sum_{i=1}^N \frac{L_i(p,\omega_i)f_r(p, w_i, w_r)(n\cdot\omega_i)}{pdf(\omega_i)} \end{aligned} \] 同时考虑直接光照和间接光照,我们就可以得到下面一个路径追踪初步的伪代码。注意其中分为直接光照和间接光照,直接光照的L直接来自于光源,间接关照的L则来自其他物体的反射,此时这个值需要递归的求解。
1 | |
注意到在这个算法中,对于一个位置p,我们需要投射N条光线,但是由于这些会出现在其他物体上的弹射,并且每次弹射也会继续有N条光线,所以很容易造成光线数量的爆炸。因此这里进行算法的改进,将N设置为1,然后将多次采样的操作设置在像素级别。于是此时的效果就是对于每个像素,我们进行多次不同方向的采样,对于每个方向只投射一根光线。由于跟踪的是一条光线的弹射,也就有点类似于在空间中跟踪这条光线的路径,这也是该算法名称路径追踪的由来。下面是改进之后的算法伪代码:
1 | |
上面的算法仍然存在问题,因为我们发现光线会在场景中一直弹射,反应在算法中就是递归没有停止条件。改进的方法是使用俄罗斯轮盘赌(Russian Roulette,RR)。考虑光线每次弹射都可能有\(p\)的概率停止弹射。当然考虑到能量守恒,如果光线停止弹射,我们需要对它的能量进行补偿,即将当前的L修正为L/p。
类似于神经网络中dropout的补偿修正。
根据RR的思想,我们可以改进shade方法:
1 | |
至此我们已经得到了一个正确的路径追踪算法,但是它仍然存在一些问题。虽然它能够得到正确的结果,但是它效率太低了。考虑光源很小的时候,只有很少的光线能够最终抵达光源,很多的采样光线都浪费了。
一种改进思路是直接对光源进行采样,假设光源面积为A。之前的渲染方程是对立体角做积分,因此在立体角上采样,现在需要对光源进行采样,那么则需要将渲染方程改写为对光源的积分,实际上就是需要找到dA和dw之间的关系:
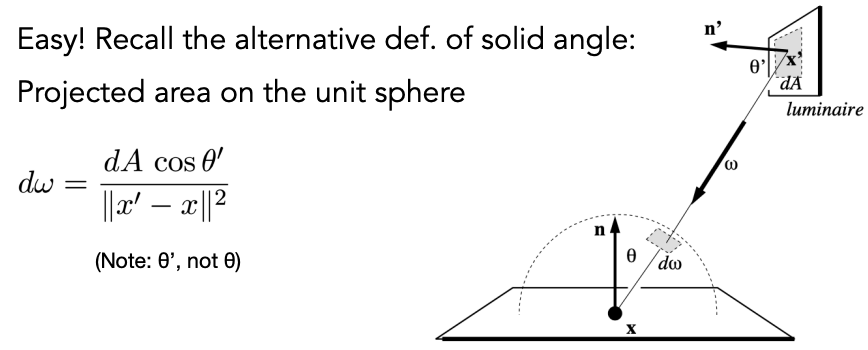
改写后的渲染方程: \[ \begin{aligned} L_o(x, \omega_r) &= \int_{\Omega+} L_i(x,\omega_i)f_r(x, w_i, w_r)\cos{\theta}d\omega_i \\ &=\int_{A} L_i(x, \omega_i)f_r(x, \omega_i,\omega_r)\frac{\cos{\theta}\cos{\theta'}}{||x'-x||^2}dA \end{aligned} \] 此时将对应的算法伪代码进行改进:
1 | |
注意上面的算法没有判断光源和点之间是否有遮挡,当然这也非常容易判断,如果判断有遮挡的话,那么就直接返回即可。