深度学习中的转置卷积
转置卷积
转置卷积(Transposed Convolution)是一种与卷积相对应的操作,它的作用是用来完成上采样upsampling。需要明确的是,转置卷积并不是卷积的逆运算。并且转置卷积不同于数学上的反卷积。
运算步骤
接下来我们介绍一下转置卷积的运算步骤。转置卷积实际上也可以看作是一种卷积操作,只不过需要进行一些前置处理。与卷积相同,转置卷积同样具有三个基本参数,stride、padding和kernel。将这三个参数简单记为s、p和k,那么转置卷积的运算步骤如下所示:
- 首先在输入特征图元素之间填充s-1行和列,填充0
- 然后在输入特征图的周围填充k-p-1行和列,同样填充0
- 将卷积核的参数上下、左右翻转
- 之后进行正常的卷积运算,不过在这个卷积运算中,对应的padding=0,strip=1
下面的动图表示的分别是s=1,p=0,k=3和s=2,p=1,k=3的情况:
(s=1,p=0,k=3)
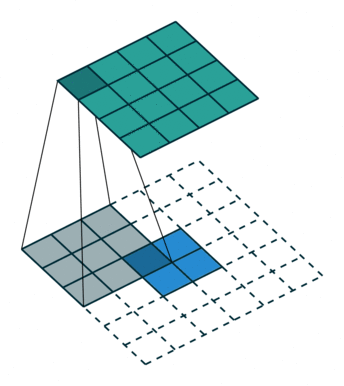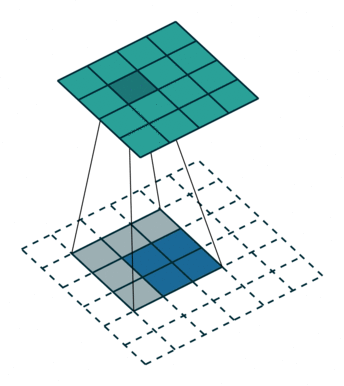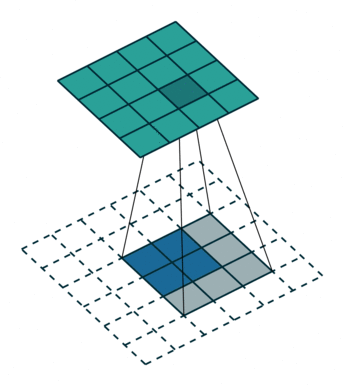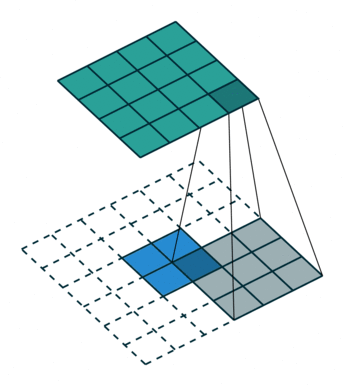
(s=2,p=1,k=3)
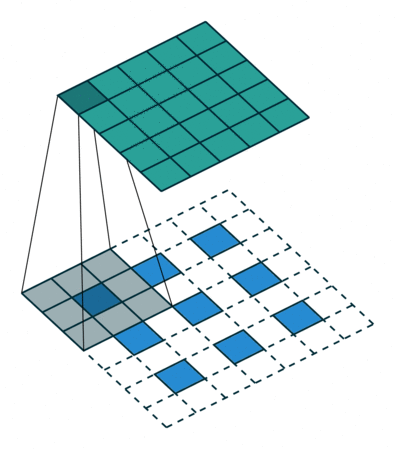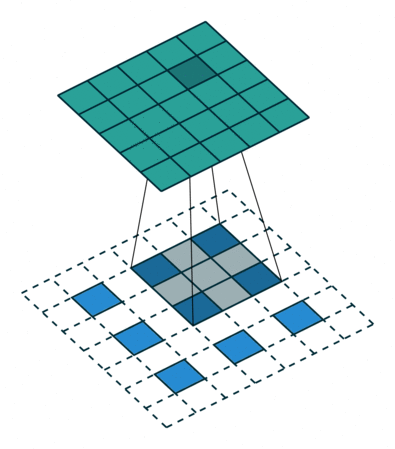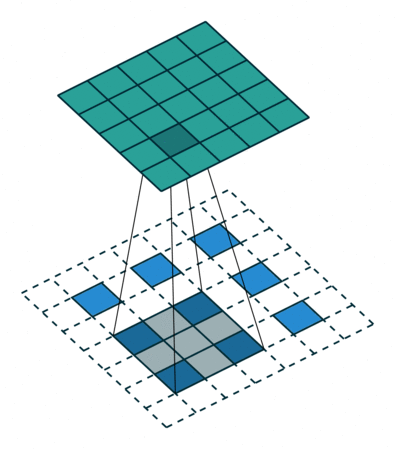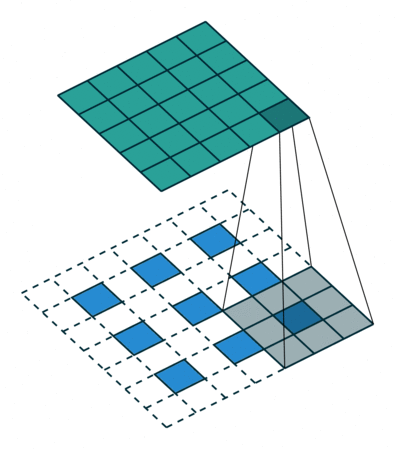
根据上面的步骤,我们也可以得到转置卷积输入前后,图像高宽之间的关系: \[ \begin{aligned} H_{out} &= (H_{in} - 1) \times stride[0] - 2 \times padding[0] + kernel\_size[0] \\ W_{out} &= (W_{in} - 1) \times stride[1] - 2 \times padding[1] + kernel\_size[1] \end{aligned} \]
Tips:可以发现,在转置卷积中,padding变大会使得输出变小,而stride变大使得输出变大。
在Pytorch中直接提供了转置卷积的API
torch.nn.ConvTranspose2d()供我们使用,详细情况可以参考:ConvTranspose2d — PyTorch 2.1 documentation。在Pytorch提供的API中,还提供对空洞卷积的适应,可以参考相关资料:吃透空洞卷积(Dilated Convolutions) - 知乎
转置卷积的理解
转置卷积和卷积具有对应关系,是因为我们可以在一定程度上将其看作是卷积的“逆运算”。但是这个“逆运算”并不是在真正的逆运算,因为它们之间不能在数值上保持一致,而是仅在形状上能够保持一致。换句话说,转置卷积不是还原值,而是还原形状。
首先回到卷积上。之前我们是从运算逻辑上,以移动窗口的形式来理解卷积的运算。但是在实际实现的时候,整个卷积是可以变成一个矩阵运算的。对于每一次滑动窗口,我们可以从卷积核出发得到一个等效矩阵。多次滑动窗口,得到多个小的等效矩阵,将小矩阵展平并以列向量的形式组成一个大等效矩阵。实际上,最终的卷积运算就是将原始特征图展成一维向量,该一维向量和这个大等效矩阵进行矩阵乘法,得到卷积后的结果。如果用式子表示,则可以表示成下面的式子,其中\(X\)表示展平后的原始特征图,\(C\)表示等效矩阵,\(Y\)表示卷积后的结果。 \[ X_{1\times r} C_{r\times c} = Y_{1\times c} \] 观察这个式子,如果我们有\(Y\)和\(C\),我们并不能保证得到\(X\)。这是因为我们不能保证\(C\)的逆矩阵存在。但是我们可以利用\(Y\)和\(C\)得到一个和\(X\)形状相同的矩阵,即计算: \[ Y_{1\times c} C^{T}_{c\times r} = X^{'}_{1\times r} \] 也就是用\(Y\)乘上等效矩阵\(C\)的转置。这也对应了Transposed Convolution中的转置。而这种理解,实际上在数学上也正好能对应前面的运算步骤,尤其是将卷积核参数上下、左右翻转,然后进行卷积。
总结来说,我们有:
转置卷积实际上也是一种卷积,它将输入和核进行了重新排列,然后进行特殊的卷积操作(stride=1, padding=0)
卷积一般来做下采样,转置卷积一般来做上采样
卷积将输入从\((h,w)\)变成\((h',w')\),在同样的超参数下,转置卷积将输入从\((h',w')\)变成\((h,w)\)。即转置卷积完成的是形状的还原
对于特定的参数,我们还是主要关注输入前后的数据形状变化,可以通过上面的公式进行计算