相机参数介绍
相机参数
在3D模型的训练过程中,通常需要在3D坐标系和图像坐标系中进行转换,此时我们会用到相机外参和相机内参。在过程中,涉及到不同的坐标系,包括世界坐标系,相机坐标系,以及图像坐标系。概括来说,通过相机外参矩阵,可以从世界坐标系转化到相机坐标系,通过相机内参矩阵,可以从相机坐标系转化到图像坐标系。(以下介绍均以针孔摄像机为例)
相机外参
相机外参矩阵(extrinsic)又可以称为w2c(world to camera)矩阵,它的作用是用作transform矩阵,将世界坐标系的3D坐标变换到相机坐标系中。该矩阵由\(3\times 3\)的正交旋转矩阵R和\(3\times 1\)的平移矢量t组成,通常也可以记作\([R|t]\),维度为\(3 \times 4\)。如果使用齐次坐标,则可以表示为\(4\times 4\)的维度,形式如下: \[ w2c = \begin{bmatrix} R & t \\ 0 & 1 \\ \end{bmatrix} \] 在齐次坐标的表达下,我们可以利用w2c矩阵来将世界坐标系的3D坐标变换到相机坐标系中,此时两个坐标系中都是3D坐标,齐次坐标表示则有4维。
另外,还有一个相机位姿(pose)的概念。相机位姿描述的是相机坐标系是如何通过世界坐标旋转和平移得来的,对应得到旋转矩阵\(R_c\)和平移矢量\(t_c\)。\([R_c|t_c]\)实际上描述的就是相机坐标系xyz轴以及相机中心在世界坐标系中的方向和位置。具体来说,旋转矩阵的第一列到第三列分别表示相机坐标系xyz轴在世界坐标系下对应的方向;平移向量表示相机原点在世界坐标系中对应的位置。 \[ [R_c|t_c] = [x_{\text{c in w}}, y_{\text{c in w}}, z_{\text{c in w}}, p_{\text{camera center in w}}] \] 实际上,我们有c2w(camera to world)矩阵,它与w2c矩阵互为逆矩阵,表示的也是互相相反的转换。c2w矩阵实际上就可以通过pose得到。在齐次坐标表示下,我们有: \[ c2w = \begin{bmatrix} R_c & t_c \\ 0 & 1 \\ \end{bmatrix}, \quad w2c = c2w^{-1} \] 通过计算,可以得到: \[ R = R_c^{T}, \quad t = -Rt_c \]
相机内参
相机的内参矩阵(intrinsic)通常可以表示为\(K\)。它的作用是将相机坐标系下的3D坐标映射到2D的图像平面。相机内参描述了相机的内部特性,包括焦距、主点位置、畸变等信息。这些参数通常是固定的,与相机的位置和方向无关。
以针孔摄像头为例,内参矩阵\(K\)如下所示: \[ K = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \] 其中\(f_x\)\(和f_y\)是相机的水平和垂直焦距在相机坐标系中的表示,单位为像素(对于理想的针孔相机,\(f_x=f_y\))。相机焦距指的是是相机中心到成像平面的距离,通常是长度单位,为了转化为像素表示,还需要结合对应的比例。\(c_x\)和\(c_y\)是图像原点相对于相机光心的水平和垂直偏移量,单位同样是像素。在一般情况下,\(c_x\),\(c_y\)可以用图像宽和高的1/2近似。
实际上标准的内参矩阵\(K\)还包括一个偏斜量skew \(s\),如下所示: \[ K = \begin{bmatrix} f_x & s & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \] 不过一般情况下,我们会假设像素没有偏斜,即\(s=0\)。
在齐次坐标的情况下,我们可以利用内参矩阵\(K\)来将相机坐标系下的3D坐标\(A\)(齐次表示具有4维)映射到图像坐标系中的2D坐标\(B\)(齐次表示具有3维度),映射关系如下: \[ B_{3\times 1} = K_{3\times 3}[I, 0]_{3\times 4} A_{4\times 1} \] > 注意这里的\(B_{3\times 1}\)最后一个维度并不一定等于1,考虑\(B=[b1, b2, b3]\),这里的\(b3\)不一定为1,实际上\(b3=z\),表示在相机坐标系中成像平面距离相机的距离。实际图像坐标系中的非齐次2D坐标则需要计算为\((u, v) = (b1/z, b2/z)\)
实际上,根据分块矩阵,如果我们不使用齐次坐标,相机坐标系下的3D坐标为\([x, y, z]\),图像坐标系中的2D坐标为\([u,v]\),那么我们有: \[ z \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = K \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} \\ \]
这种方式直接将\(K\)理解为从相机坐标系的非齐次坐标转换到像素坐标系的齐次坐标。
通过相机的内参和外参,我们就可以得到相机的投影矩阵(Projection matrix)\(P\)。通过投影矩阵,我们可以将世界坐标系中的点映射到二维图像平面,实际也就是依次连续使用世界坐标系->相机坐标系->图像坐标系的变换(依次左乘变换矩阵),我们有: \[ \begin{aligned} P &= K[I,0] w2c = K[I, 0]\begin{bmatrix} R & t \\ 0 & 1 \\ \end{bmatrix} \\ & = K[R|t] \end{aligned} \]
至此我们可以进行一个阶段性总结:
- 相机外参(extrinsic, w2c)\([R|t]\),它的作用是将世界坐标系的3D坐标变换到相机坐标系中
- 相机位姿(pose, c2w),描述的是世界坐标系如何通过旋转和平移得到相机坐标系,这对应一个pose矩阵。这个pose矩阵在数值上与相机外参互逆(在齐次形式下)。
- 相机内参(intrinsic)\(K\),它的作用是将相机坐标系下的3D坐标映射到2D的图像平面中
另外,相机参数的获取一般有两种方式。一般对于公开的数据集,其中都直接包含了相机参数,虽然组织形式有所区别,需要查看对应的文档。对于一些真实场景数据集,例如我们自己使用手机拍摄了一组图像,想要获取相机位姿,则可以通过Structure-From-Motion(SFM, 运动恢复结构)技术来估计几个相机之间的相对位姿,其中最为常用的软件是COLMAP。通过输入多张图片,COLMAP可以估计出相机的内参和外参。
坐标系变换
假设某个像素点在像素坐标系下的坐标为\((u,v)\),该像素点对应的实际点在相机坐标系下的坐标为\((x,y,z)\),该像素点对应实际点在世界坐标系下为\((X_W,Y_W,Z_W)\),同时相机的内参为\(K\),相机的外参表示为\(R,t\),那么我们有: \[ z \begin{bmatrix} u\\ v \\ 1 \end{bmatrix} =K_{3\times 3} [R_{3\times3}|t_{3\times1}]_{3\times 4} \begin{bmatrix} X_W \\ Y_W \\ Z_W \\ 1 \end{bmatrix} \\ \] 如果已知\((X_W, Y_W, Z_W)\),我们可以很容易推算出\((u,v)\)。反之,如果有\((u,v,z)\)的话,我们也可以反过来推算\((X_W,Y_W, Z_W)\),即从相机坐标系转回世界坐标系。注意这里需要知道该像素点在相机坐标系中的深度\(z\)。如果不知道深度信息,则只能计算出一个光线方向,表示该像素点对应的实际点在这条射线上。
计算方式如下: \[ \begin{aligned} z \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} &= K \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} ,\quad 可以得到 \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} = K^{-1}z \begin{bmatrix} u \\ v \\ 1\\ \end{bmatrix} \\ \end{aligned} \] 然后根据上面的整体投影公式,可以得到: \[ \begin{bmatrix} x \\ y \\ z\\ \end{bmatrix} = R\begin{bmatrix} X_W \\ Y_W \\ Z_W\\ \end{bmatrix} + t, \quad 因此 \begin{bmatrix} X_W \\ Y_W \\ Z_W\\ \end{bmatrix} = R^{-1}\begin{bmatrix} x \\ y \\ z\\ \end{bmatrix} - t \] 当然,由于我们已经知道了相机坐标系中的\((x, y, z)\),那么也可以在转化为齐次坐标之后,利用c2w矩阵,计算出齐次坐标下的世界坐标。
常用坐标系
下面介绍一些常用的相机坐标系,实际上就是明确成像平面的坐标系,包括OpenCV坐标系和OpenGL坐标系。
注意这些都是相机坐标系。
人眼向图像中看去,其中:
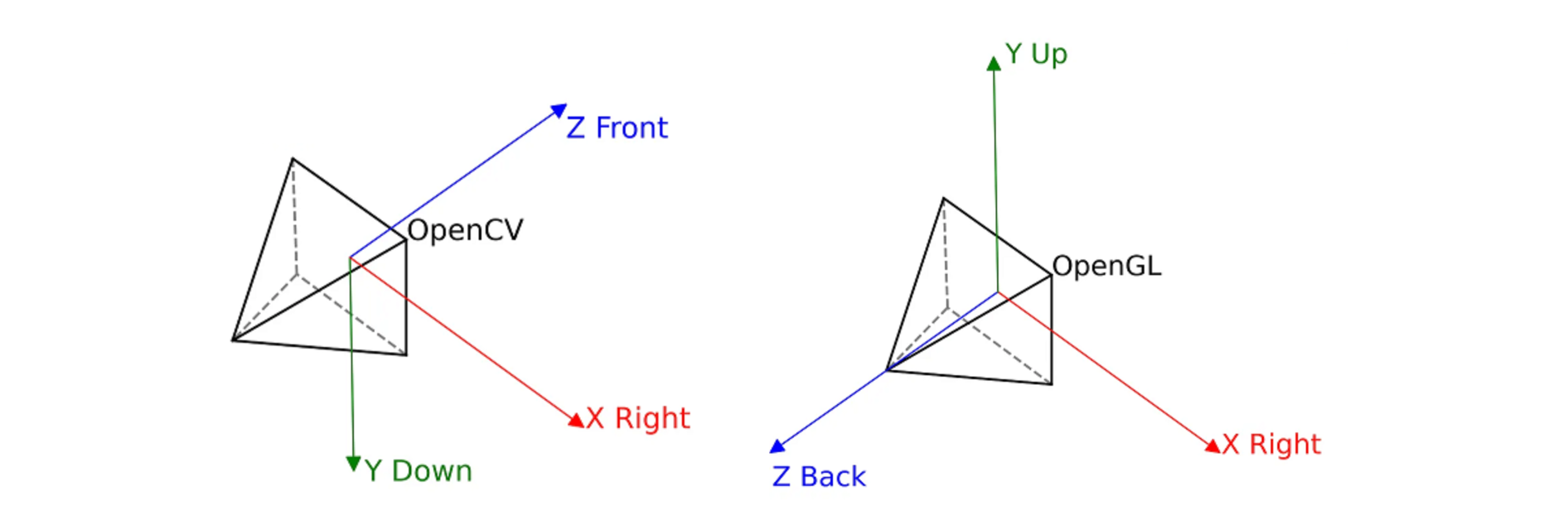
- OpenCV坐标系:z轴指向前方,x轴指向右方,y轴指向底部
- OpenGL坐标系:z轴指向自己,x轴指向右方,y轴指向上方
OpenCV和OpenGL坐标系相互转化的时候相当于z轴和y轴需要反转。
- NerfStudio中采用的相机坐标系是OpenGL坐标系。
- Colmap中采用的相机坐标系是OpenCV坐标系。
考虑在OpenCV相机坐标系下,我们有\(c2w_{opencv}\);如果使用OpenGL相机坐标系描述,对应有\(c2w_{opengl}\),那么我们有,实际上就是YZ轴的反转: \[ c2w_{opencv}[0:3, 1:3] * -1 = c2w_{opengl} [0:3, 1:3] \]
进行转换的代码:
1 | |
畸变参数
上面我们考虑的是标准的成像模型,但是在实际操作过程中,可能会发生畸变。在相机标定中,使用畸变参数来描述这种畸变。
畸变分为径向畸变和切向畸变,径向畸变可以使用畸变系数\(k_1, k_2, k_3\)来描述(一、二、三阶径向畸变系数),切向畸变可以使用畸变系数\(p_1,p_2\)来描述(一、二阶切向畸变系数)。
对于拍摄的图像点\((x,y)\),有了畸变系数之后,我们就可以对它进行校正,得到校正后的点\((x',y')\)。计算公式如下: \[ \begin{aligned} \text{径向畸变模型:} & r = \sqrt{x^2+y^2}\\ & x_d = x (1+k_1r^2+k_2r^4 + k_3r^6) \\ & y_d = y (1+k_1r^2+k_2r^4+k_3r^6) \\ \text{切向畸变模型:} & x' = x_d + [2p_1xy+p_2(r^2+2x^2)] \\ & y' = y_d + [p_1(r^2+2y^2)+2p_2xy] \end{aligned} \] 当然在OpenCV中可以直接调用相关方法来进行畸变校正:
1 | |