动手学深度学习(6)-循环神经网络
循环神经网络
循环神经网络(Recurrent Neural Network, RNN),它的提出是为了解决一些需要考虑上下文的信息的问题。在网络的计算过程中,它会用到之前的信息。RNN使用隐藏层来记录过去发生的所有事件的信息,从而引入时序的特征,同时潜变量\(h_t\)的使用可以避免常规序列模型当中每次都要重新计算前面所有已经发生的事件从而带来的计算量。
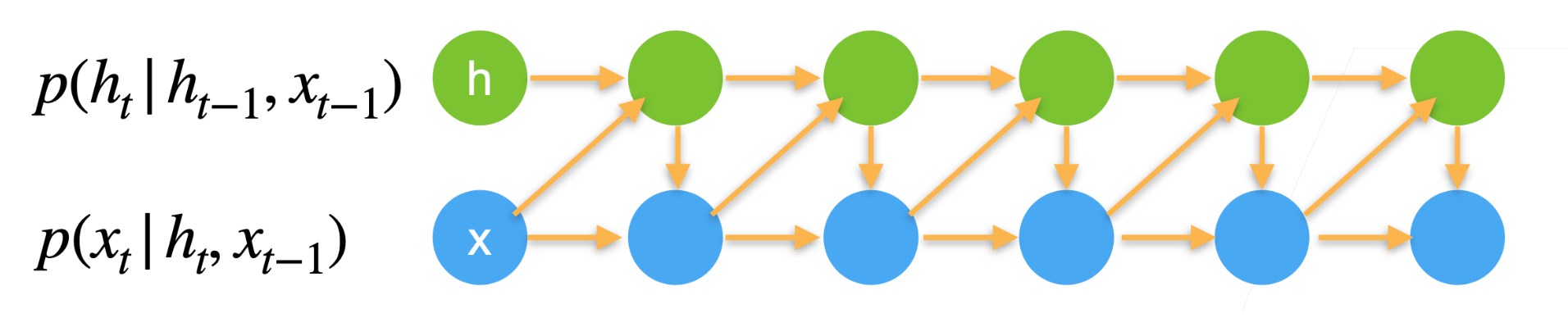
具体来说,首先我们拥有一个输入序列,目前希望得到\(t\)时刻的输出。那么我们会用前一时刻即\(t-1\)时刻的输入\(x_{t-1}\)和潜变量\(h_{t-1}\)来计算得到当前时刻的潜变量\(h_t\),然后再利用它计算得到当前时刻的输出\(o_t\) \[ \begin{aligned} h_t &= \phi(W_{hh}h_{t-1} + W_{hx}x_{t-1} + b_h) \\ o_t &= \phi(W_{ho}h_t + b_o) \end{aligned} \]
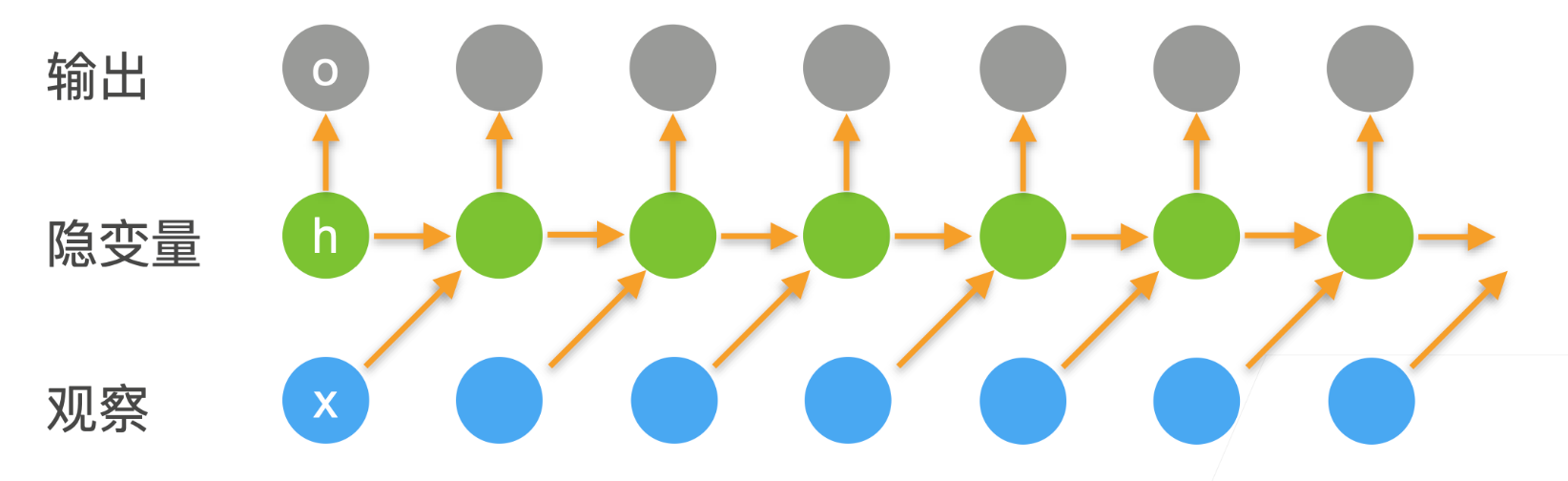
实际上RNN的本质也还是一种MLP,它的核心就在于潜变量的使用,它使得模型可以在一定程度上记录过去的信息,储存时序信息。可以理解为RNN就是包含时序信息的MLP。
GRU
GRU名称为Gated Recurrent Unit,意为门控循环单元。门控循环单元与普通的循环神经网络之间的关键区别在于,前者支持隐状态的门控。这意味着模型有专门的机制来确定应该何时更新隐状态,以及应该何时重置隐状态。
在GRU中有两个组件,分别是重置门Reset Gate和更新门Update Gate,重置门主要用来控制遗忘,即当前输出是否需要考虑前一隐藏状态;更新门主要用来控制关注,即是否需要根据当前输入来更新隐藏状态。(门的概念是借助于电路中的一个概念,01代表不同的电平,可以用来控制电路的通断。)这里重置门和更新门拥有对应的可学习的参数,即下面式子中的\(W\),然后通过sigmoid将其设置到01范围内。实际上重置门和更新门的表达式是完全相同的,只是分别使用了两套学习参数,我们在逻辑上认为能够达到对应的效果。 \[ \begin{aligned} R_t &= \sigma(X_tW_{xr} + H_{t-1}W_{hr} + b_r) \\ Z_t &= \sigma(X_tW_{xz} + H_{t-1}W_{hz} + b_z) \end{aligned} \]
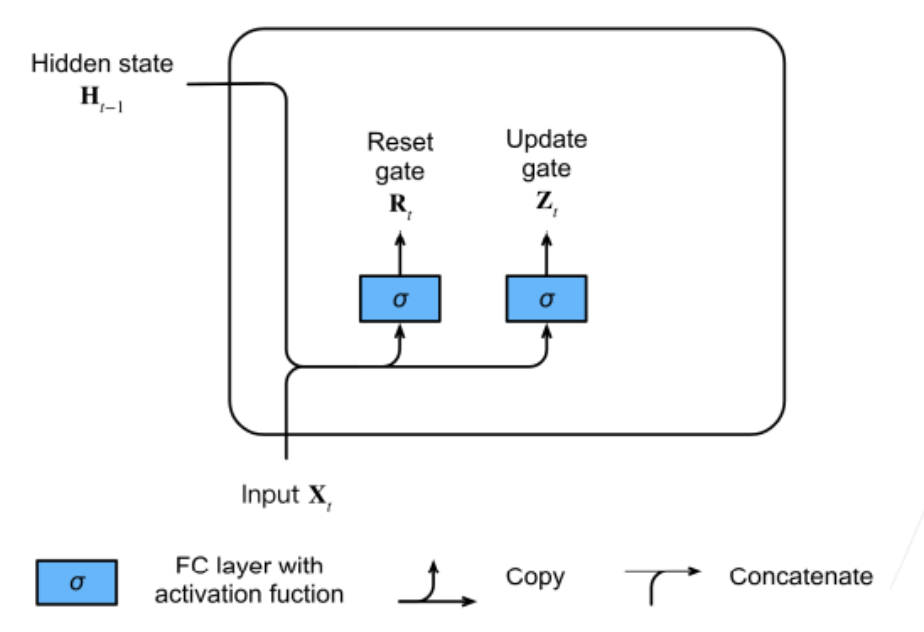
接下来我们需要根据重置门\(R_t\)和更新门\(Z_t\)来计算得到当前时刻下的隐藏状态\(H_t\)。这里分为两步进行计算,首先根据重置门\(R_t\)得到候选隐藏状态\(\widetilde{H}_{t}\),然后根据更新门\(Z_t\)得到最终的隐藏状态。计算方式如下: \[ \begin{aligned} \widetilde{H}_{t} &= \tanh (X_tW_{xh} + (R_t \odot H_{t-1})W_{hh} + b_h) \\ H_t &= Z_t \odot H_{t-1} + (1 - Z_t) \odot \widetilde{H}_{t} \end{aligned} \]
LSTM
LSTM,全称为Long Short-term Memory,意为长短期记忆。
LSTM (Long Short-term Memory),它本质上还是一个短期的记忆(Short-term Memory),只不过这个短期的记忆比较长(Long)
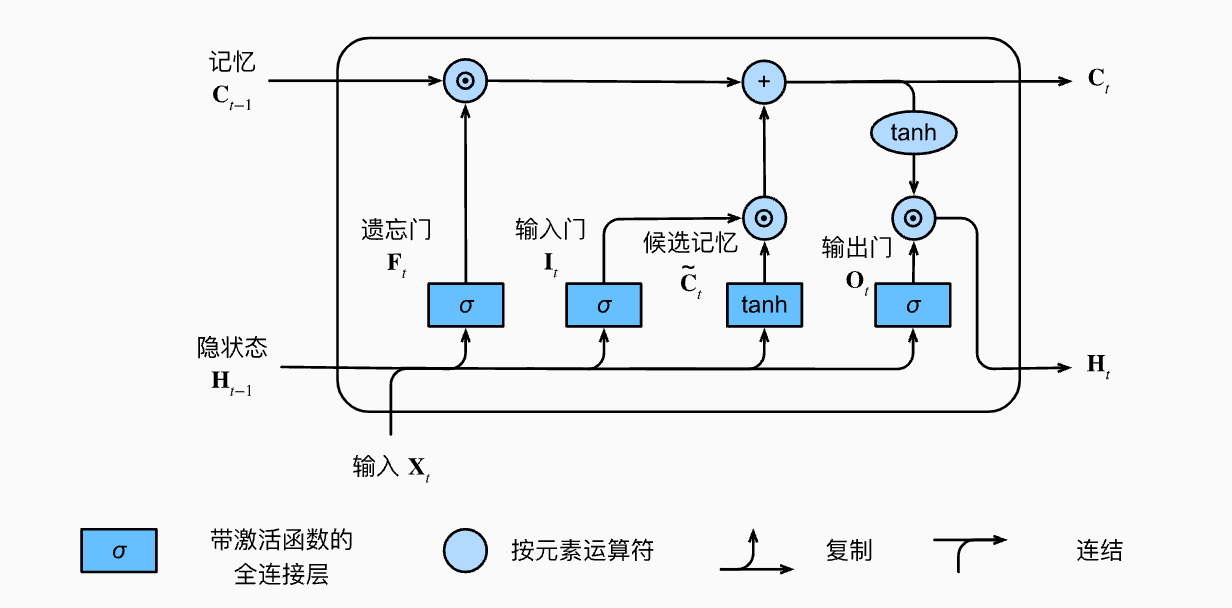
在LSTM中包含三个门控单元,分别是输入门Input Gate、输出门Output Gate和遗忘门Forget Gate。其中输入门控制是否需要忽略当前输入数据、输出门控制是否需要使用隐状态、遗忘门控制是否需要清空隐状态。
三个门控的值计算方式类似于上面GRU中的两个门控值: \[ \begin{aligned} I_t &= \sigma(X_tW_{xi} + H_{t-1}W_{hi} + b_i) \\ F_t &= \sigma(X_tW_{xf} + H_{t-1}W_{hf} + b_f) \\ O_t &= \sigma(X_tW_{xo} + H_{t-1}W_{ho} + b_o) \end{aligned} \] 同时,LSTM中也有候选记忆元\(\widetilde{C}_t\)的概念,它的计算与上面的三个门类似,但是使用tanh函数作为激活函数,函数值范围为\((-1, 1)\): \[ \widetilde{C}_t = \tanh(X_tW_{xc} + H_{t-1}W_{hc} + b_c) \] 在LSTM中,输入门控制采用多少来自当前候选记忆元的新数据、遗忘门则控制保留多少过去记忆元的内容,由此得到新的记忆元: \[ C_t = F_t \odot C_{t-1} + I_t \odot \widetilde{C}_t \] 而输出门则控制如何更新当前时刻的隐状态\(H_t\),计算方式如下。只要输出门接近1,我们就能够有效地将所有记忆信息传递给预测部分;而如果输出门接近0,我们则只保留记忆元内的所有信息,而不需要更新隐状态。 \[ H_t = O_t \odot \tanh(C_t) \] LSTM状态更新的全流程可以参考下图: