动手学深度学习(7)-注意力机制与Transformer
注意力机制简介
背景介绍
在心理学中有一个双组件的框架,它描述是说受试者往往会基于非自主性提示和自主性提示来有选择的引导自己的注意力。举例来说,假设我们面前有五个物品,分别是一份报纸、一篇研究论文、一杯咖啡、一本笔记本和一本书,其中所有的纸制品都是黑白印刷的,而咖啡杯是红色的。在这个环境中,人们往往会一眼就注意到那个红色的咖啡杯,或者说这个红色的咖啡杯在环境中是突出和显眼的。这就是非自主性提示。在喝过咖啡之后,我们会变得兴奋并且想要读书,此时就会有目的地去寻找书本。此时选择书是受到了认知和意识的控制,也就是自主性提示。
如果以这种方式定性地去考察网络结构,可以说类似于卷积、全连接、池化层等结构考虑的都是非自主性的提示,而注意力机制考虑就是自主性提示。
考虑环境由多组键值对构成,而自主性提示就是对应的query。注意力机制通过注意力汇聚(Attention Pooling)来最终得到一个输出,这个输出是考虑了自主性提示query而得出来的。注意力机制可以根据query来有偏向地选择某些输入。因此我们可以看出,注意力机制实际上需要做到的就是如何根据环境(Key-Value键值对)以及自主性提示(Query)来有偏好地得到最终的输出。即下面的计算如何完成。 \[ f(q;(k_1, v_1), ..., (k_n,v_n)) \]
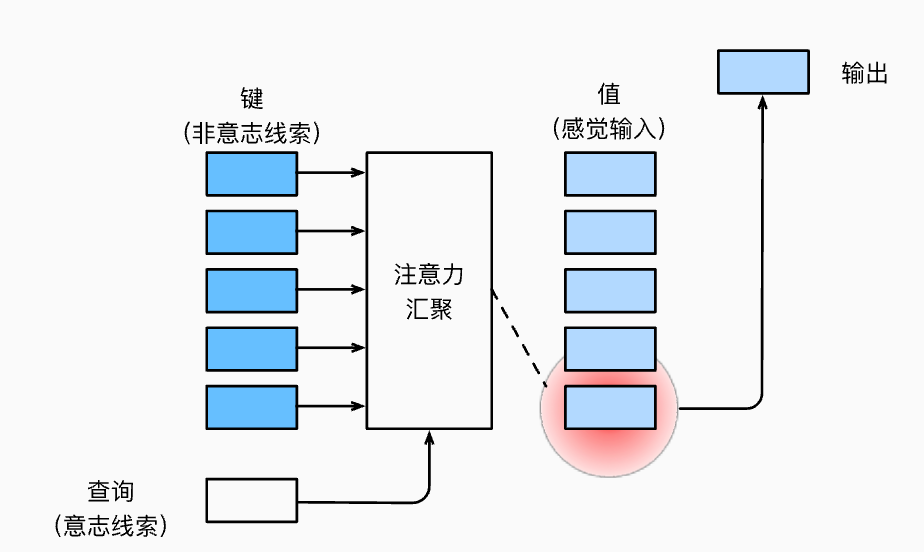
非参数的注意力机制
首先考虑非参数的注意力机制,即不带有其他可学习参数的机制。那么最简单的方法就是平均池化: \[ f(q) = \frac{1}{n} \sum_{i} v_i \] 显然这种方式并没有q和k的参与,于是更好的方案实际上是60年代提出的Nadaraya-Watson 核回归,其中K表示Kernel核函数,利用核函数来对各个value进行加权平均: \[ f(q) = \sum_{i=1}^{n} \frac{K(q-k_i)}{\sum_{j=1}^n K(q-k_j)}v_i \] 假设我们使用高斯核\(K(u) = \frac{1}{\sqrt{2\pi}} \exp(-\frac{u^2}{2})\)作为核函数,那么上面的式子可以进行如下展开: \[ \begin{aligned} f(q) &= \sum_{i=1}^{n} \frac{\exp(-\frac{1}{2} (q - k_i)^2)}{\sum_{j=1}^{n} \exp(-\frac{1}{2} (q - k_j)^2)} v_i \\ &= \sum_{i=1}^{n} \text{softmax}(-\frac{1}{2} (q - k_i)^2) v_i \end{aligned} \]
参数化的注意力机制
上面我们说的是非参数的注意力机制,其中没有任何可以学习的参数。要将其改造成参数化的注意力机制也非常容易,只需要在其中增加一个可以学习的参数\(w\)即可: \[ f(q) = \sum_{i=1}^{n} \text{softmax}(-\frac{1}{2} ((q - k_i)w)^2) v_i \] 受此启发,我们可以重新描述注意力机制框架中需要完成的任务,即设计如下计算公式: \[ f(q) = \sum_{i=1}^n \alpha(q, k_i)v_i \] 其中\(\alpha(q, k_i)\)表示注意力权重,如何设计权重的计算也就是不同注意力机制完成的事情。
注意力分数
上面我们说到使用高斯核的注意力计算方式,即: \[ f(q) = \sum_i \alpha(q, k_i)v_i = \sum_{i=1}^n \text{softmax}(-\frac{1}{2} (q-k_i)^2)v_i \] 这里引入注意力分数的概念,注意力分数是没有经过标准化的注意力权重。注意力权重范围是0-1,注意力分数则没有范围限制。这里\(-\frac{1}{2} (q-k_i)^2\)表示注意力评分函数,根据q和k计算出对应的注意力分数。注意力分数经过softmax之后得到标准化之后的注意力权重。因此我们可以进一步进行重写,我们需要设计对应的注意力评分函数\(a(q,k_i)\),它没有输出范围的限制,而注意力权重\(\alpha(q,k_i)\)就是评分\(a\)经过softmax之后得到的值。理论上,注意力评分函数应该能够刻画q和k之间的相关性。 \[ \begin{aligned} f(q, (k_1, v_1), ..., (k_n, v_n)) &= \sum_{i=1}^{n} \alpha(q, k_i) v_i \in \mathbb{R}^v\\ \alpha(q, k_i) = \text{softmax} (a(q, k_i)) &= \frac{\exp(a(q, k_i))}{\sum_{j=1}^{m}\exp(a(q,k_j))} \in \mathbb{R} \end{aligned} \] 接下来则介绍两个注意力评分函数,分别是加性注意力和缩放点积注意力。
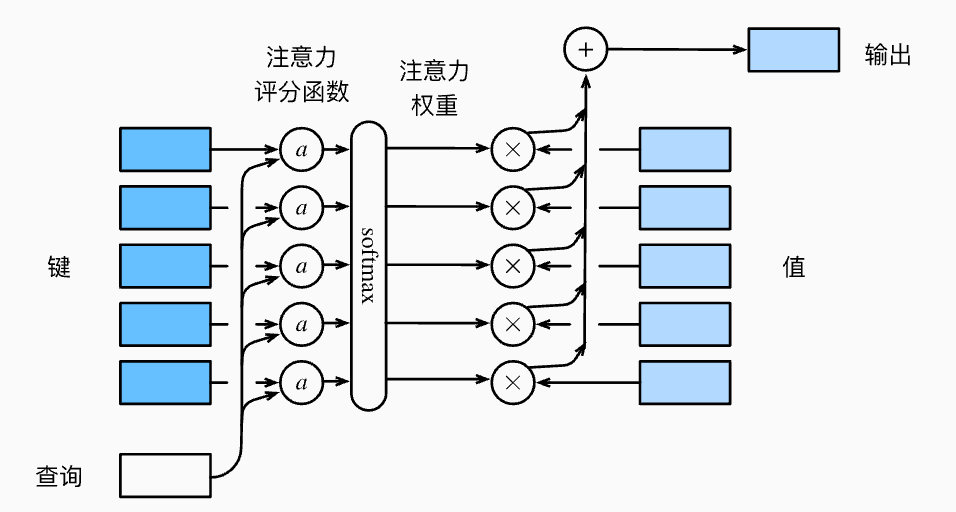
加性注意力
一般来说,当query和key是不同长度的向量的时候,我们可以使用加性注意力作为评分函数。给定query \(\mathbf{q} \in \mathbb{R}^q\)以及 key \(\mathbf{k} \in \mathbb{R}^k\),加性注意力(Additive Attention)的评分函数为: \[ a(\mathbf{q}, \mathbf{k}) = \mathbf{w}_v^T \tanh(\mathbf{W_q}\mathbf{q} + \mathbf{W_k}\mathbf{k}) \in \mathbb{R} \] 其中包括可学习的参数\(\mathbf{W}_q \in \mathbb{R}^{h \times q}, \mathbf{W}_k \in \mathbb{R}^{h \times k},\mathbf{w}_v \in \mathbb{R}^{h}\)。
这种计算方式实际上就等价于将query和key合并起来然后输入到一个隐藏层大小为\(h\),输出大小为\(1\)的单隐藏层MLP中。
缩放点积注意力
如果query和key是具有相同长度的向量,那么使用点积(内积)则可以得到计算效率更高的评分函数。给定query \(\mathbf{q} \in \mathbb{R}^d\)以及 key \(\mathbf{k} \in \mathbb{R}^d\),那么缩放点积注意力的评分函数为: \[ a(\mathbf{q}, \mathbf{k}) =\frac{<\mathbf{q}, \mathbf{k}>}{\sqrt{d}} \] 在实际应用的过程中,我们通常会使用小批量向量化的版本。考虑查询query \(\mathbf{Q} \in \mathbb{R}^{n\times d}\),key \(\mathbf{K} \in \mathbb{R}^{m\times d}\)和value \(\mathbf{V} \in \mathbb{R}^{n\times v}\),则缩放点积注意力为: \[ f(\mathbf{Q}) = \text{softmax}(\frac{\mathbf{Q}\mathbf{K}^T}{\sqrt{d}}) \mathbf{V} \in \mathbb{R}^{n\times v} \]
多头注意力机制
在实践中,当给定相同的query、key和value的集合,我们希望模型可以基于相同的注意力机制学习到不同的行为,然后将不同的行为作为知识组合起来,依次捕获各种依赖关系。因此我们可以使用多头注意力机制,即对于相同的query、key和value,我们首先通过独立学习,得到h组不同的投影。这h组投影是通过独立学习的不同全连接层变换而来的。之后这h组变换之后的query、key和value被并行地送到Attention Pooling中,得到h组输出。最后将这h个输出拼接在一起,然后再进行后续的处理。
基于这种设计,每个头都可能会关注输入的不同部分, 可以表示比简单加权平均值更复杂的函数。
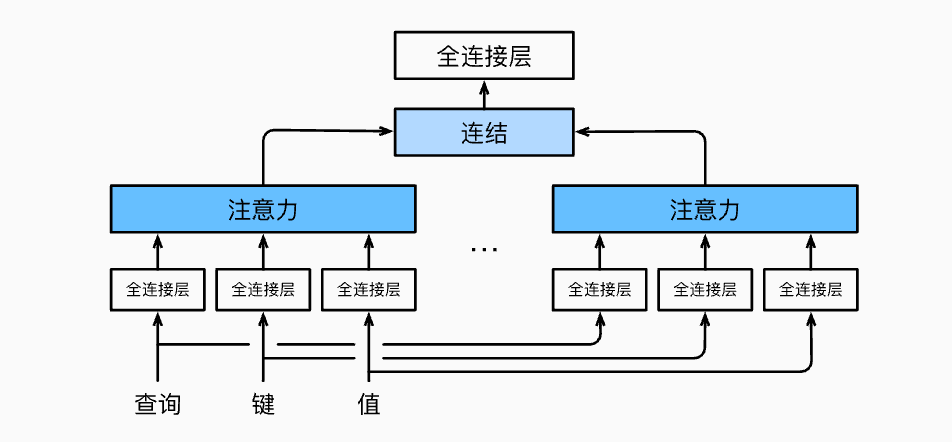
自注意力机制与位置编码
自注意力机制
前面我们提到,注意力机制中包括\(\mathbf{q},\mathbf{k},\mathbf{v}\)等概念,这些qkv在不同情况下可能指代模型中的不同成分。一种特殊的情况是三者都是同一个\(\mathbf{x}\),这也就是自注意力机制。
具体来说,对于给定输入序列\(\mathbf{x}=\{x_1, x_2, ..., x_n\}, x_i\in \mathbb{R}^d\),自注意力机制就是利用这个\(\mathbf{x}\)同时充当\(\mathbf{q},\mathbf{k},\mathbf{v}\),计算方式为: \[ y_i = f(x_i, (x_1, x_1), ..., (x_n,x_n)) \in \mathbb{R}^d \]
自注意力机制可以对一个序列进行特征抽取,而无序其他query,key,value的参与,它接受接受一个序列,输出另外一个序列。
在小批量向量化的情况下,则有: \[ f(\mathbf{X}) = \text{softmax}(\frac{\mathbf{X}\mathbf{X}^T}{\sqrt{d}})\mathbf{X} \] 但是在实际运用的过程中,可能会对\(\mathbf{X}\)增加可学习的参数,先做不同的线性变换之后再输入(例如Transformer): \[ f(\mathbf{X}) = \text{softmax}(\frac{\mathbf{X}\mathbf{W_Q}\mathbf{X}^T\mathbf{W_K}}{\sqrt{d}})\mathbf{X}\mathbf{W_V} \]
- CNN,RNN和Self-Attention的对比
注意到,CNN、RNN和Self-Attention三者都可以完成序列到序列的操作,输入一个序列,输出为另一个同样长度的序列,但是它们三者存在一定的区别。我们假定输入和输出的序列长度为\(n\),输入和输出的通道数都是\(d\):
- 对于CNN来说,假定卷积核大小为\(k\)。由于对于每个输出,都需要利用卷积核进行一次计算,通道之间进行相乘,因此它的计算复杂度为\(O(knd^2)\)。由于每个输出是可以单独计算的,因此它的并行度是\(O(n)\)。考虑输入序列中两个相隔较远的值产生联系需要的最长路径,可以知道最长路径为\(O(n/k)\)
- 对于RNN来说,在更新隐藏状态的时候,需要\(d\times d\)权重矩阵和\(d\)维隐状态的乘法,因此整体的计算复杂度为\(O(nd^2)\)。RNN考虑时序信息,因此无法进行并行计算,并行度为\(O(1)\)。最长路径为\(O(n)\)
- 对于Self-Attention来说,查询、键和值都是\(n\times d\)矩阵。对于每个输入,都需要和其他所有的输入进行注意力分数的计算,计算的时候复杂度为\(d\),因此总体的计算复杂度是\(O(n^2d)\)。同样每个输出是可以单独计算的,因此并行度是\(O(n)\)。而最长路径为\(O(1)\)
至此我们可以对自注意力机制进行一个简单的总结:
- 自注意力池化层将\(\mathbf{x}\)当作注意力机制中的query、key、value,来对序列进行特征抽取
- 自注意力机制可以做到完全并行,并且最长序列为1,但是对于长序列来说,计算复杂度会非常高
位置编码
自注意力机制中最长序列的长度是1,这表示在序列中相隔很远的两个元素,在计算的时候实际上并没有相隔很远,也就是说在自注意力机制中并没有记录位置信息。
位置编码就是说我们希望将位置的信息引入到自注意力机制中。为了保留自注意力机制的并行计算优势,我们并不改变自注意力本身的计算方式,而是选择直接将位置信息进行编码,然后添加到输入当中。具体来说,假设一个长度为\(n\)的序列\(\mathbf{X}\in \mathbb{R}^{n\times d}\),那么我们会先计算出一个位置编码矩阵\(\mathbf{P} \in \mathbb{R}^{n\times d}\),然后使用\(\mathbf{X}+\mathbf{P}\)作为自注意力的输入。
因此核心就是位置编码矩阵如何计算,不同应用领域对位置编码的设计可能有所不同,这里介绍在Transformer中使用的位置编码方式: \[ p_{i,2j} = \sin(\frac{i}{10000^{2j/d}}), \quad p_{i, 2j+1} = \cos(\frac{i}{10000^{2j/d}}) \] 这种编码方式的好处在于可以同时表示绝对位置和相对位置。对于绝对位置来说,可以类比二进制的表示方式,此种位置编码方式使用三角函数在编码维度上降低频率,由于输出是浮点数,因此此类连续表示比二进制表示法更节省空间。对于相对位置来说,此种位置编码方式可以很简单的表示相对位移。对于任何确定的位置偏移\(\delta\),位置\(i+\delta\)处的位置编码可以通过\(i\)处的位置编码线性变换得到,令\(w_i = 1/10000^{2j/d}\),则有: \[ \begin{bmatrix} p_{i+\delta, 2j}\\ p_{i+\delta, 2j+1} \end{bmatrix} = \begin{bmatrix} \cos (\delta w_j) & \sin(\delta w_j)\\ -\sin (\delta w_j) & \cos(\delta w_j) \end{bmatrix}\begin{bmatrix} p_{i,2j}\\ p_{i,2j+1} \end{bmatrix} \]
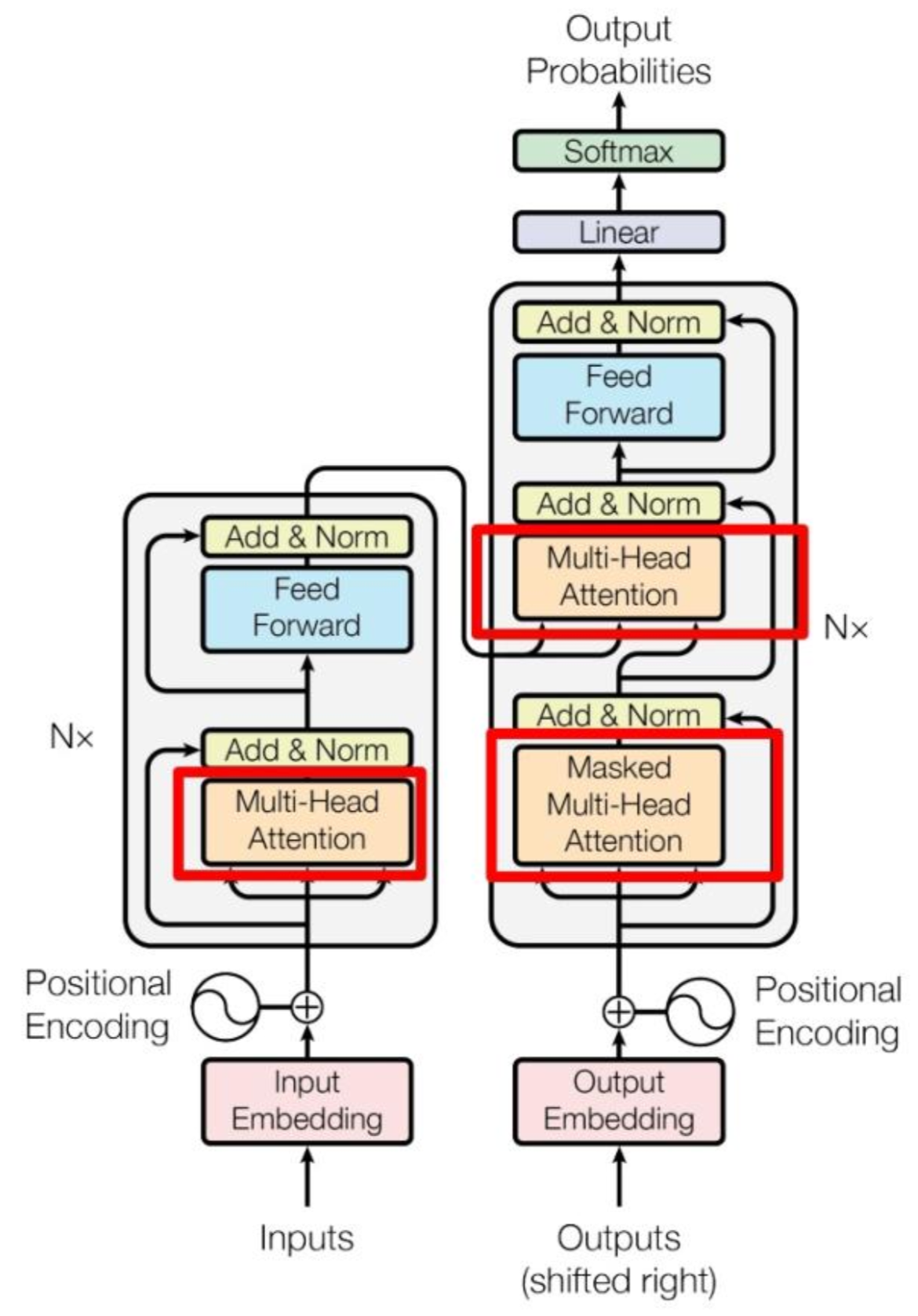
Transformer
Transformer基于Encoder-Decoder架构来处理序列对,它的架构图如下: