Mulit-View Stereo 传统方法
MVS基础知识
MVS,全称为Multi-View Stereo,多视角立体视觉。MVS可以帮助我们完成三维重建,三维重建指的是用相机拍摄真实世界的物体、场景,并通过计算机视觉技术进行处理,从而得到物体的三维模型。而MVS也正是利用场景的多张图片来恢复场景的3D结构。常见的MVS开源框架包括:colmap、MVE、PMVS、SMVS、OpenMVS等。
对于MVS来说,它的输入是多张图片(以及每张图片对应的相机参数),输出是3D模型。
MVS基本的pipeline可以参考下面的过程:
图像收集(多视角图片) -> 相机参数恢复(特征提取与匹配+稀疏重建) -> 3D场景重建(稠密重建) -> 场景材质的重建
MVS的输出是3D模型,常见的3D结构表示形式包括深度图、点云、voxel以及mesh,因此MVS也可以根据其输出的不同对应划分为不同的类别,如下图所示。
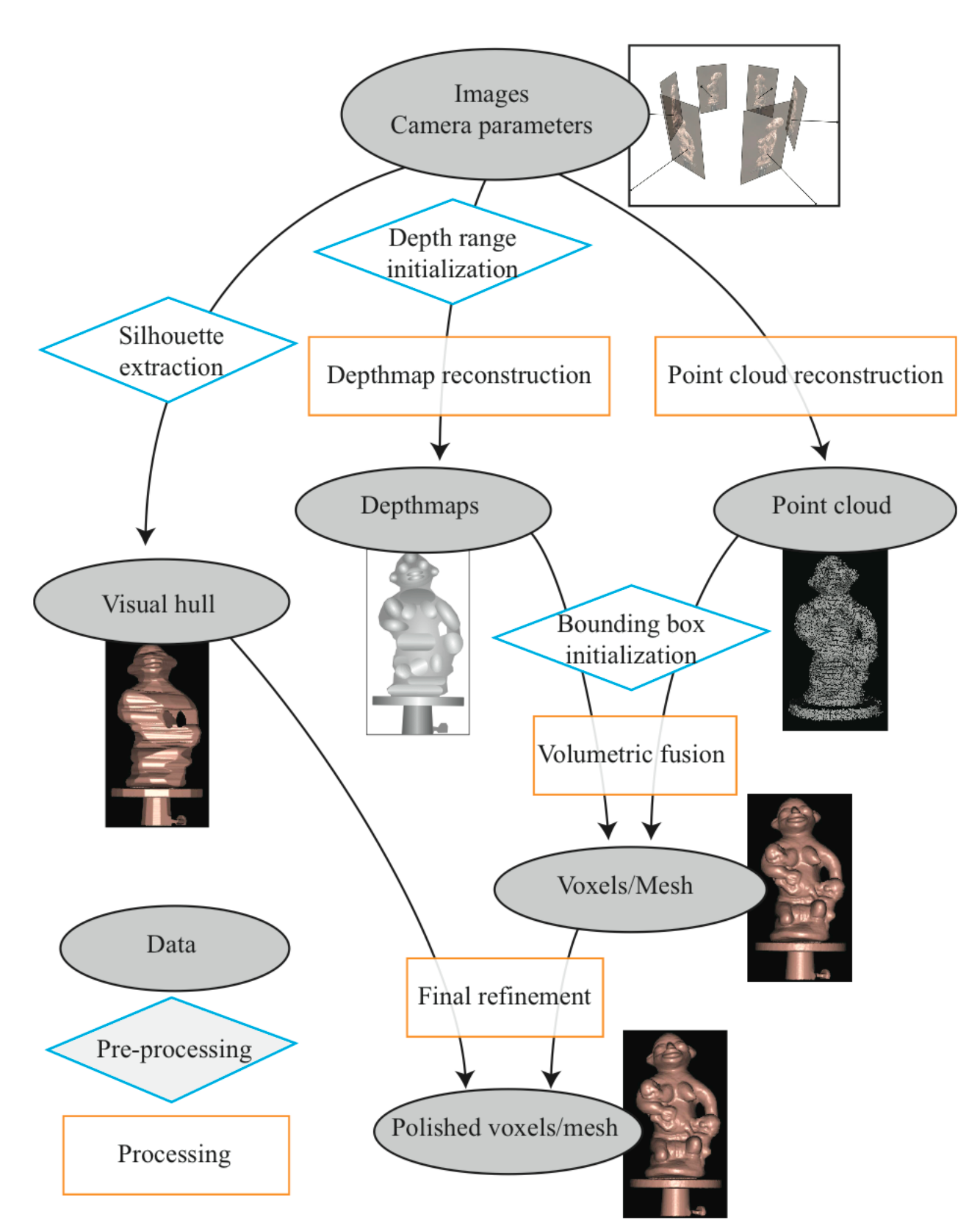
当然不同的3D表示之间也可以相互转化,例如可以利用多场景的深度图来过滤融合构建场景的点云、利用深度图得到voxel表达、利用点云得到mesh表达等。
图像收集
MVS的输入就是多张图像,那么首先需要拿到图像。根据拍摄环境的不同,图像数据基本可以分为三类,分别是实验室环境下拍摄图片、室外小场景以及大规模场景图片。其中,根据拍摄时相机是否有序,则又可以分为有序图像序列以及无序图像序列。
可用于MVS的图像数据集包括:
- Middlebury Stereo Dataset:vision.middlebury.edu/stereo/data
- DTU Dataset:MVS Data Set – 2014 | DTU Robot Image Data Sets
- Tanks and Templates:Tanks and Temples Benchmark
- ETH3D:Datasets - ETH3D
- ScanNet:ScanNet | Richly-annotated 3D Reconstructions of Indoor Scenes
- BlendMVS:YoYo000/BlendedMVS: BlendedMVS: A Large-scale Dataset for Generalized Multi-view Stereo Networks
- GigaMVS:GigaVision
- KITTI:The KITTI Vision Benchmark Suite
- ...
相机参数恢复
MVS的第二步需要进行相机参数的恢复,在这一步中,我们需要利用多张图片,得到每一张图片对应的相机参数信息。MVS算法结果的质量很大程度上取决于输入图像和相机参数的质量。根据图像是否有序,相机参数的恢复可以分为两类:
- 有序图像相机参数的恢复:VSLAM(视觉同步定位与建图,Visual Simultaneous Localization and Mapping)
- 无序图像相机参数的恢复:SfM(运动恢复结构,Structure-from-Motion)
这里我们简单介绍一下SfM。SfM的输入是一组图像,输出则是每个图像对应的相机参数+一系列3D坐标(以及它们对应在图像中的像素坐标),其中3D坐标可以构成一系列轨迹Track。支持完成SfM的常用框架包括colmap、MVE、openMVG等。
SfM常见的过程如下:
- 首先在每张输入图片之中检测2D的特征,例如角点等;
- 然后在图片之间进行2D特征的匹配;
- 通过特征匹配pair来构建2D的跟踪轨迹;
- 通过2D轨迹来构建SfM模型
- 利用Bundle Adjustment来优化SfM模型
Bundle Adjustment(捆绑调整)是一种在计算机视觉和摄影测量学中广泛使用的优化技术,主要用于同时精确估计相机的三维姿态(位置和方向)和场景结构的过程。Bundle Adjustment的核心思想是通过最小化重投影误差来优化相机参数和场景点的三维坐标。重投影误差是指三维点投影回相机成像平面后的位置与其原始观测位置之间的差异。
MVS对重投影误差非常敏感,因此如果SfM的结果需要用到MVS上,那么通常都需要应用Bundle Adjustment。不过需要注意的是,重投影误差是以像素为单位进行测量的,因此可以对输入图像进行下采样并重新调整相机参数,直到重投影误差下降到某个阈值以下,只需要下采样的图像仍然包含足够的纹理和细节即可。
立体匹配
与MVS任务相近的任务是立体匹配。双目立体匹配要求我们使用一个场景在不同视角下的图像来还原3D场景结构。可以说MVS是双目立体匹配的自然改进,MVS重建算法中很多相关的原理都起源于立体匹配。在MVS的问题背景下,相机参数是已知的,此时求解场景的3D几何形状完全等价于求解输入图像之间的对应问题。接下来我们主要介绍双目立体匹配如何还原场景的深度图。
同名点寻找
考虑两张图片,我们可以记为Reference和Target,这两张图是对同一场景的不同拍摄。考虑空间中的一个点,它会在这两张图中分别投影到某个像素上,这种代表同一空间点的两个像素点称为同名点。在立体匹配任务中,我们首先需要找到这些同名点对。
考虑Reference中的某个像素A,和Target中的某个像素B,我们要如何判断A与B是否是同名点呢?由于我们只有图像信息,因此只能通过像素的相似度进行衡量。衡量两个像素的相似度的方法被称为代价函数,常用的代价函数包括Squared intensity Differences(SD)、Absolute intensity Differences(AD)、Normalized Correlation Coefficient(NCC)、Census Transform(CT)、Birchfield-Tomasi's cost(BT)、Mutual Information(MI)等。这里我们不对代价函数进行展开叙述,我们只需要知道代价函数可以帮助我们衡量两个像素之间的相似度,相似度越高,匹配代价越小。
那么为了找到两张图片之间的同名点对,我们可以利用匹配代价函数。对于Reference中的像素A,我们可以依次遍历Target中的每个像素,计算它与像素A之间的匹配代价,匹配代价最小的那个像素即为像素A的同名对。这的确是一种方式,但是这种方式会带来非常高的复杂度,此时我们可以引入对极几何中的知识。当多个摄像机从不同视点观看同一3D场景时产生的不同几何约束称为对极几何。
由于两张图片是对同一场景不同角度下的拍摄,因此同名点会满足极线约束(Epipolar constraint),即像素A在Target中的同名点只会出现在一条其中的一条极线上,因此我们没有必要考虑整张图中所有的像素,只需要考虑极线上的像素即可。利用极线约束,我们就可以将搜索空间从2维降低到1维。
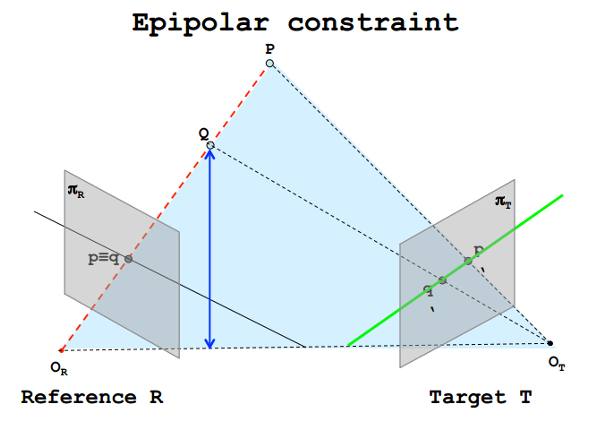
视差与深度
上面我们提到,可以使用极线约束来降低搜索空间。而为了让计算更加方便,我们通常还会进行极线纠正,实际上就是将两个像平面进行旋转等变化,将两个像平面变换到与Baseline平行的平面上,让两个相机的主光轴相互平行。这样可以使得极平面与两张影像的交线位于图像的同一行,这样同一极线对位于两张图片的同一行,即同名点对的行号一定相等,只存在列号的差异。
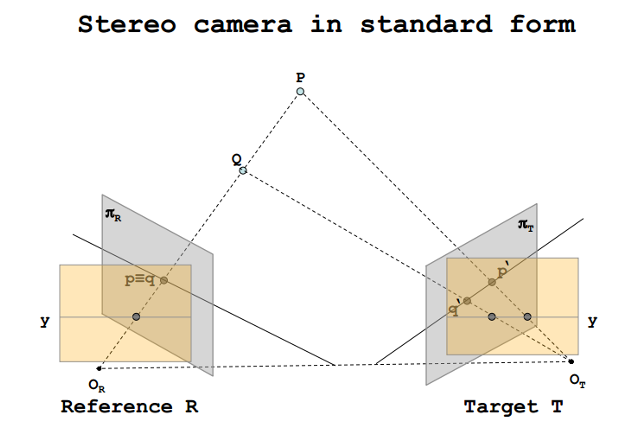
经过极线纠正之后,两个同名点之间仅存在列号上的差异,这种差异就被称为视差(广义的视差具有行视差和列视差)。考虑在经过极线纠正之后,两张图中的同名点对的列坐标分别为\(X_R,X_T\),那么视差\(d\)就定义为: \[ d = X_R-X_T \] 严格来说,这个视差是定义在Reference图上的。也就是说,针对Reference上的每个像素,都会有一个对应的视差\(d\),通过这个视差就可以得到同名点坐标。这种存储每个像素视差值的图像叫做视差图(disparity map),以像素为单位。与视差图概念类似的还有深度图(depth map),这也是我们立体匹配最终需要还原的输出。深度图中每个像素存储的实际上是原图中该像素位置对应3D点的深度,以实际长度为单位。
视差和深度实际上是可以相互转换的,视差图可结合基线和相机内参计算出深度图。我们考虑如下的双目成像过程,其中\(p,p'\)表示一对同名点,\(x_l,x_r\)表示它们对应的列坐标。那么对于左视图来说,\(p\)对应的视差就是\(d = x_l - x_r\)。
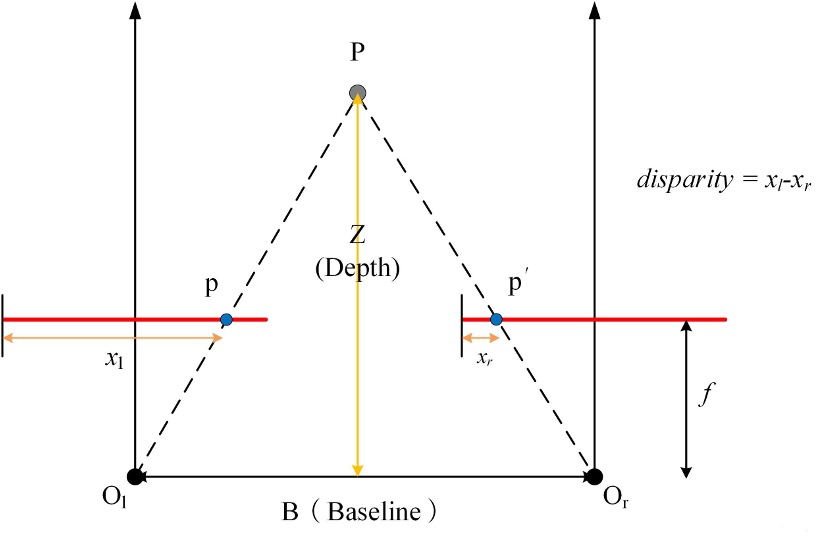
通过简单的三角形相似,我们可以计算出Depth: \[ D = \frac{Bf}{d + (x_{Or} - x_{Ol})} \] 由于在一般情况下,我们都认为光心对应位于图像的中心点,因此\(x_{Or}=x_{Ol}\),所以有: \[ D = \frac{Bf}{d} \] 通过这个公式,我们就可以完成视差图和深度图之间的转换。我们也可以定性的评估深度与视差之间的关系:
- 深度值越大,视差值越小。
- 深度值越大,同样的视差范围,对应的深度范围也越大。
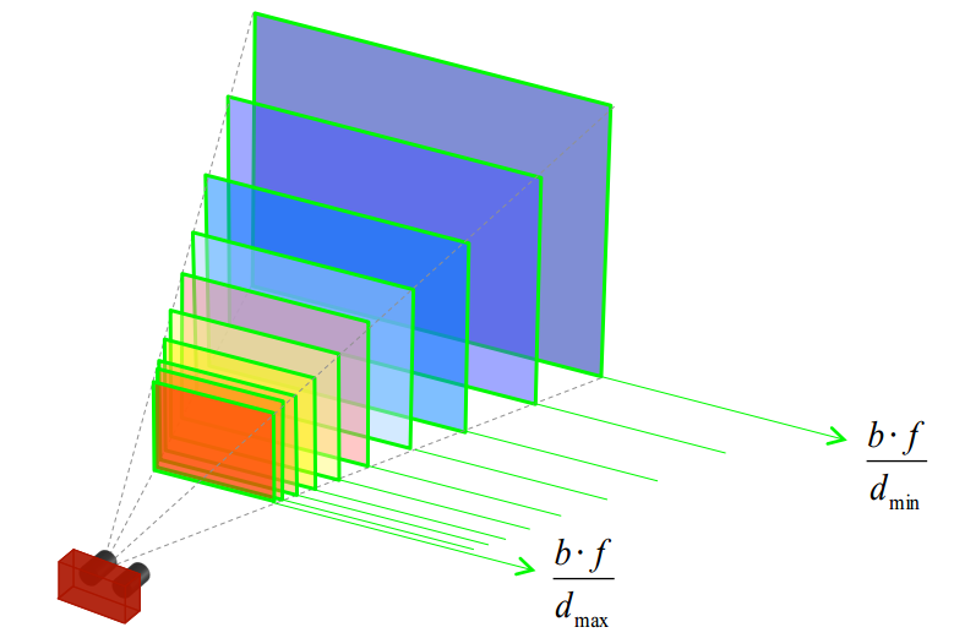
DSI
那么重新回到立体匹配的问题上来,为了重建出深度图,我们可以先构建视差图。也就是说,我们需要确定对于Reference的每个像素A,它的视差是多少。同样,视差的确定也是通过同名点的确定得到的。对于Reference中的每个像素A,我们可以先假定它的视差是\(d’\),由此我们可以得到像素A对应的同名点,从而计算出匹配代价。之后,对于一定范围内的每个视差,我们都可以得到一个匹配代价,之后就可以基于这些匹配代价来确定最终的视差,当然选择其中匹配代价最小的作为最终的视差值是一种最简单的想法。
这里需要需要提到一点,在进行立体匹配之前,我们会对场景的深度首先进行粗略的估计,确定一个深度范围,得到场景的最大和最小深度。有了深度范围,也就可以确定视差范围,上面所说的“一定范围内的每个视差”也就是值得这个视差范围。通常对应到程序实现中,我们会在这个视差范围内进行均匀采样,作为所有可能的候选视差。
同样在实现方面,我们会计算一个DSI,全称为Disparity Space Image。这是一个3D的矩阵。考虑输入的图尺寸是\(H\times W\),候选视差为\(D = {d_1, d_2, ..., d_D}\),那么这个DSI的维度就是\(D\times H \times W\)。DSI实际上就是保存了每个像素在每个视差下的匹配代价,例如DSI在\((d,h,w)\)坐标下的值表示的含义就是对于Reference中\((h,w)\)坐标下的像素,它在视差为\(d_d\)的时候对应的匹配代价。有了DSI,我们就得到的了所有的匹配代价,基于此就可以继续进行视差图的还原。
pipeline
现在,我们可以再来总结一下传统立体匹配的全流程。立体匹配的全流程可以参考下面这张图:
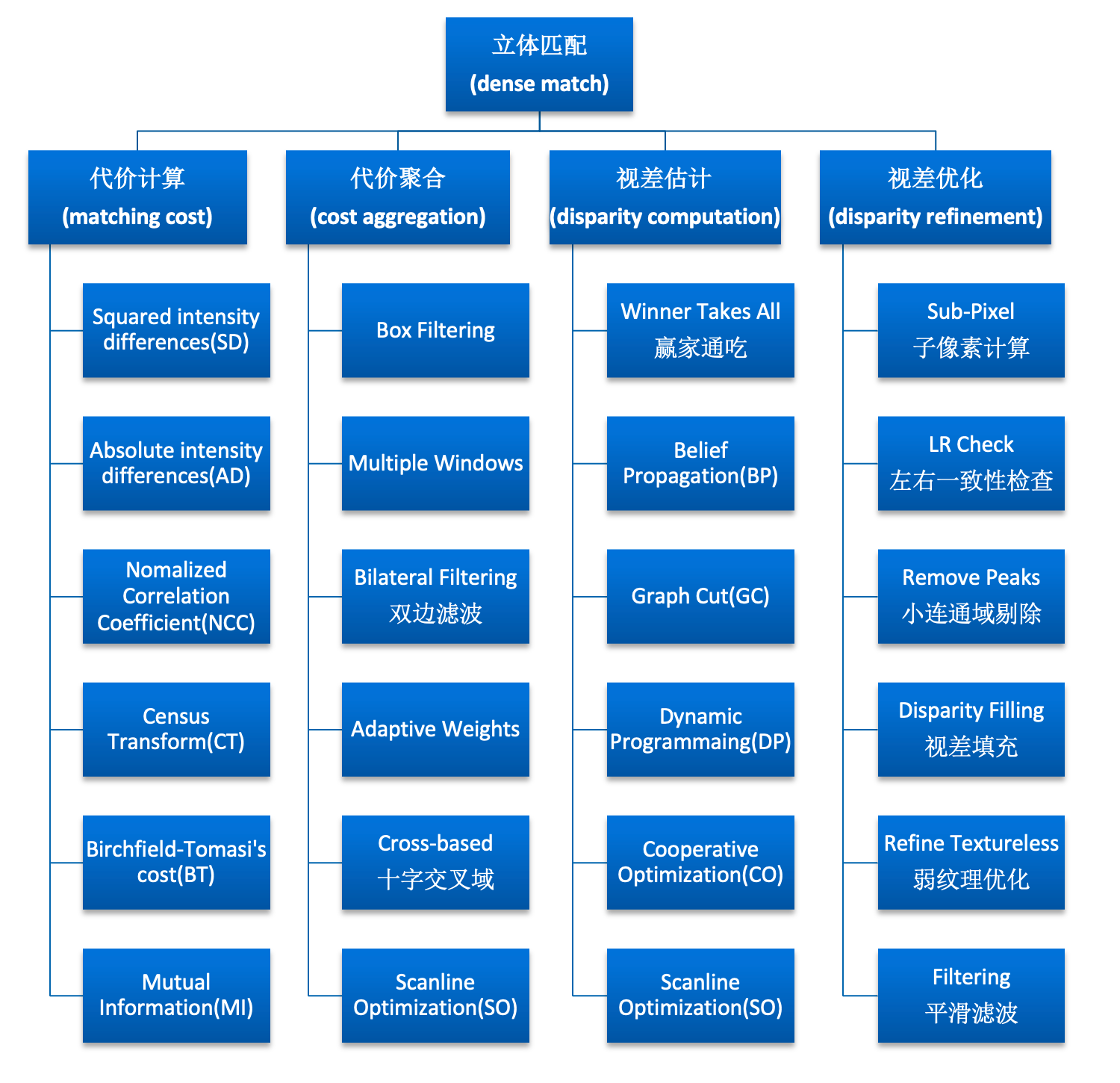
对于立体匹配的输入两张图,我们可以先进行代价计算,即计算出DSI,之后可以进行视察估计。视差估计中常用的方法就是Winner Takes All赢者通吃方法,它表示选择匹配代价最低的那个视差作为最后的输出视差。但是这种方式由于只考虑了局部,因此得到的视差图会具有较多的噪声,因此通常会在前面首先进行代价聚合,使得最终的匹配代价变得更加平滑。立体匹配的算法分为局部、全局和半全局等,其中局部方法多用Winner Takes All方法,而其他全局的方法已经考虑了全局,因此通常不会使用代价聚合。在完成了视差估计之后,通常还会执行视差优化的步骤,用来得到更加精细的视差图。
传统方法存在的问题
上面我们简单介绍了MVS的传统流程,但是传统方法存在一定的问题。可以看到算法的关键在于同名点对的确定,但是图像之间存在很多问题会影响同名点的寻找,包括亮度不一致、表面过曝、角度变化、弱纹理或无纹理、透明、遮挡、非朗伯表面等。