NeRF以及系列工作介绍(1)

Introduction

资源列表

NeRF论文跟踪项目：

awesome-NeRF/awesome-NeRF: A curated list of awesome neural radiance fields papers

评价指标

常用的评价指标包括PSNR、SSIM、LPIPS等

PSNR

PSNR代表峰值信噪比（Peak Signal-to-Noise Ratio）。它是一种用于衡量图像或音频信号质量的指标。PSNR的值越高，表示信号的质量越好，因为信噪比越大。然而，需要注意的是，PSNR并不总是完全反映人眼对图像质量的感知，特别是在一些应用场景中，如图像压缩。PSNR的计算方式如下： \[ PSNR = 10\cdot \log_{10}(\frac{MAX^2}{MSE}) \] 其中，\(MAX\)是信号的最大可能取值，对于8位图像来说，这个值是255；\(MSE\)是均方误差，表示两张图像之间每个像素差异平方的平均值。

SSIM

SSIM指的是结构相似性指数（Structural Similarity Index，简称SSIM）。SSIM是一种用于衡量两幅图像相似程度的指标，它考虑了亮度、对比度和结构三个方面的信息。SSIM值的范围是[-1, 1]，值越接近1表示两幅图像越相似。计算方式如下： \[ SSIM(x,y) = \frac{(2\mu_x\mu_y + C_1)\cdot(2\sigma_{xy} + C_2)}{(\mu_x^2 + \mu_y^2 + C_1)\cdot(\sigma_x^2 + \sigma_y^2 + C_2)} \] 其中，\(\mu_x\)和\(\mu_y\)分别是两张图像的亮度均值；\(\sigma_x^2\)和\(\sigma_y^2\)分别是两张图像的亮度方差；\(\sigma_{xy}\)是两张图片的亮度协方差；\(C_1 = (k_1L)^2,C_2 = (k_2L)^2\)是为了稳定性而添加的常数，其中\(L\)是动态范围的最大可能值，通常为1；\(k_1,k_2\)是常数，通常取\(k_1 = 0.01,k_2 =0.03\)。

LPIPS

LPIPS代表“Learned Perceptual Image Patch Similarity”（学习的感知图像块相似性），是一种衡量图像相似性的指标，不同于传统的SSIM和PSNR等指标，LPIPS更加注重图像内容的感知质量，尝试更接近于人类视觉系统的评价方式。

LPIPS通过学习的方式来评估两幅图像之间的视觉相似性。它利用深度学习模型（通常是预训练的卷积神经网络）来提取图像的特征表示，然后计算这些特征之间的差异，从而得到一个衡量图像视觉相似度的分数。这种方法认为，如果两幅图像在高层特征表示上更接近，那么它们在视觉上也应该更为相似。LPIPS的优点在于它能够更好地捕捉到人类视觉系统对于图像质量变化的敏感度，比如在纹理、细节等方面的变化，这些是传统指标（如PSNR和SSIM）难以准确评估的。

公开数据集

常用的公开数据集包括：

nerf_llff_data：NeRF使用的真实世界场景数据，一共有8个场景，包括兰花、化石、公园座椅等场景
nerf_synthetic：NeRF使用的合成数据集，一共有8个场景，包括经典乐高挖掘机、绿色椅子、船等场景
nsvf_synthetic: NSVF使用的合成数据集，一共有8个场景，具有更加复杂的几何以及光照效果
mip-NeRF 360：包括9个场景（5个室外+4个室内），每个场景都是围绕某个中间物体然后旋转360度进行拍摄，包括经典自行车等场景
RealEstate10K：一个大型视频图片数据集，包含来自YouTube视频的连续场景图片，同时包含了相机运动姿势轨迹，这些相机轨迹是通过SLAM和Bundle Adjustment计算得出的
DTU Dataset：在实验室环境中拍摄的场景，同时包括参考的点云信息和表面重建信息
Tanks and Temples：真实场景数据，包括室内和室外场景
BlendedMVS：用于广义多视图立体网络的大规模MVS数据集，包含17k个MVS训练样本，涵盖113个场景，包括建筑、雕塑和小物体等

NeRF(ECCV2020)

模型架构

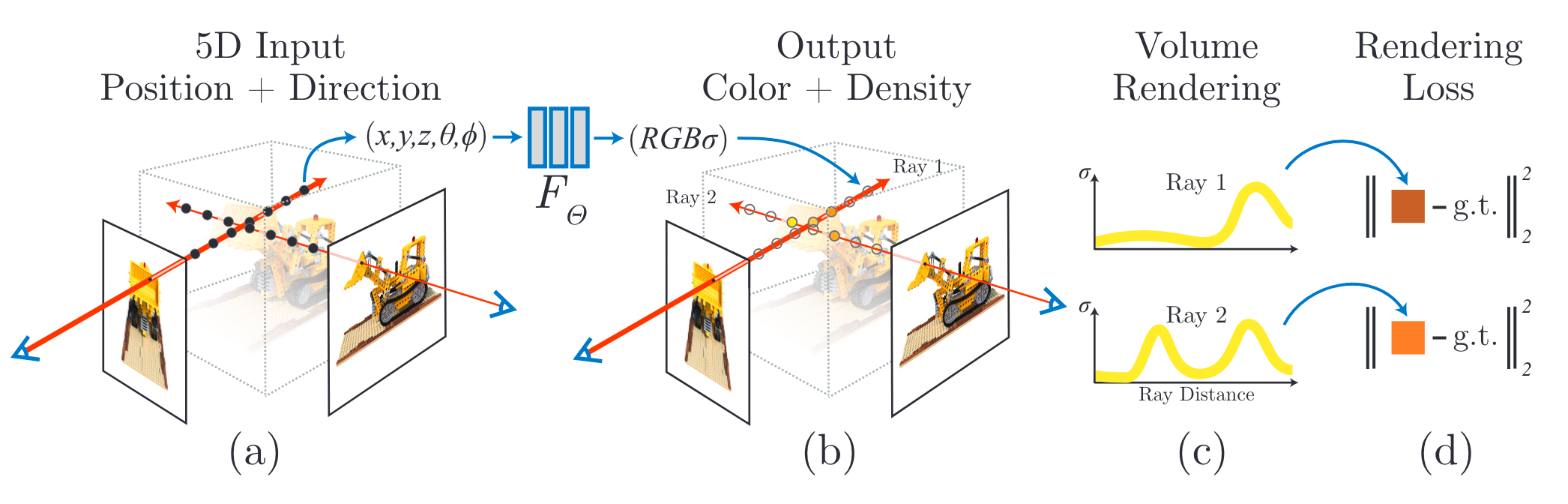
NeRF(ECCV2020)使用神经辐射场来对整个三维场景进行建模。首先是辐射场的概念，辐射场是定义在空间中的函数，记录了空间中每个点的体密度\(\sigma\)以及该点在每个方向上的颜色值\(C\)。于是三维场景就通过坐标值\((x,y,z)\)+体密度(\(\sigma\))+观察角度\((\theta,\phi)\)看到的颜色值\(C\)来表示。由于空间中有无数个点，普通函数无法建模这样的过程，因此使用神经网络来进行建模，称为神经辐射场。此时，这个神经网络的输入就是\((x, y, z, \theta, \phi)\)，输出就是\((C,\sigma)\)。当然这里的这里的xyz和观察角度都是相对于世界坐标系而言的。

这里\(\theta\)是俯仰角，\(\phi\)是偏航角。实际上对于旋转的表示还有一个滚转角，但是对于射线来说滚转角没有意义

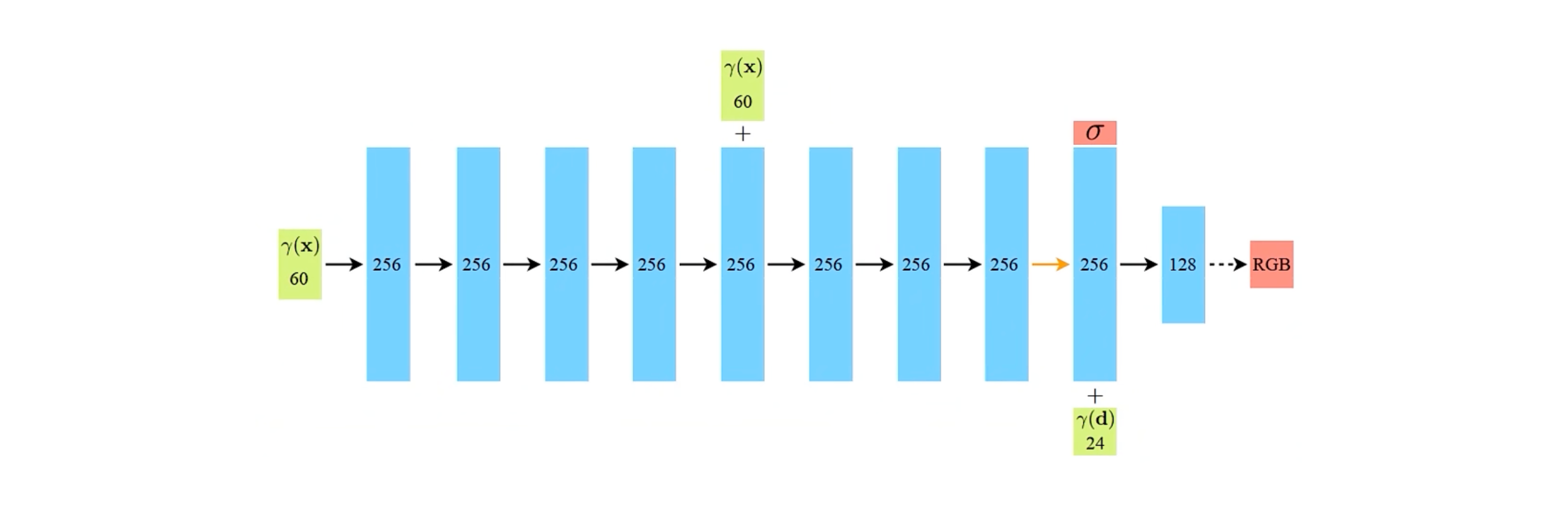
上面是NeRF使用的神经网络的结构。这里神经网络就是一个简单的多层全连接网络。对于这个神经网络来说，它的作用是记录辐射场信息：

输入：坐标位置\(\mathbf{x}\)的位置编码以及视角向量\(\mathbf{d}\)的位置编码
输出：在坐标位置\(\mathbf{x}\)的体密度\(\sigma\)以及视线\(\mathbf{d}\)方向观察时\(\mathbf{x}\)处的RGB值(范围0-1)

为什么需要视角信息：否则可能丢失反光信息

为什么需要位置编码：否则可能丢失高频几何和纹理细节

这里的高频指的是图像中连续像素变化较为剧烈的地方，神经网络会偏向于学习低频信息，而增加位置编码可以提供高频信息

NeRF使用的位置编码如下，其中位置编码越靠前差异越小越靠后差异越大变化越大，位置编码类似二进制

\[ \gamma(p) = (\sin(2^0\pi p), \cos(2^0\pi p), \dots, \sin(2^{L-1}\pi p), \cos(2^{L-1}\pi p)) \]

有了由神经网络表述的三维场景表达之后，我们就可以利用体渲染技术来进行成像。体渲染是传统图形学中的一个概念，它指的是视线上所有的点投射到图像上形成像素颜色的过程。于是，对于给定的视角，我们就可以通过体渲染技术来获得该视角下对场景的成像图片，利用成像图片和GT之间进行Loss计算，即可用模型训练。经过迭代得到较好的场景表达之后，也可以用相同的过程完成任意视角的成像。

在实际实现中，我们需要使用离散化的表达方式，其中涉及到射线上点的采样。NeRF使用两个相同的网络来进行场景的学习，第一个coarse粗网络使用的采样方式是分层采样。经过第一个coarse网络，我们可以得到一个输出。但是由于场景中区域只会集中在视线的某个部分，而分层采样可能会导致采样无法集中在该区域中，因此第二个fine细网络采用更加“明智”的采样策略。具体来说，根据离散化的体渲染方程，我们可以得到一个PDF，分段分布函数，即这里的\(w\)经过正规化使得和为1，它表示射线上的点权重沿射线变化的函数： \[ C_c(\mathbf{r}) = \sum_{i=1}^{N_c} w_i c_i, \quad w_i = T_i(1 - \exp(-\sigma_i \delta_i)) \] 通过这个函数，我们可以大体判断视线方向上物体的分布。此时这个PDF函数就可以看成是一个概率分布，然后我们通过逆变换采样(Inverse Transform Sampling)进行采样得到采样点\(N_f\)个点，与上一步coarse中\(N_c\)个采样点一同进行这一轮的优化。

逆变换采样（Inverse Transform Sampling）是一种从任意概率分布中生成随机样本的方法。它基于累积分布函数（CDF）的性质，能够将均匀分布的随机样本转换为目标分布的随机样本。这种方法的核心思想是利用均匀分布与目标分布之间的关系，通过逆变换的方式获得目标分布的样本。

NeRF中使用的损失函数是渲染颜色与真实像素颜色之间的误差，同时考虑coarse网络和fine网络： \[ L = \sum_{\mathbf{r} \in \mathcal{R}} [ || C_c({\mathbf{r}) -C(\mathbf{r})} ||_2^2 + || C_f({\mathbf{r}) -C(\mathbf{r})} ||_2^2] \]

体渲染Volume Rendering

首先考虑成像过程，视线可以表示为一条射线，视线上的点则可以表示为： \[ \mathbf{r}(t) = \mathbf{o} + t\mathbf{d} \] 其中，\(\mathbf{o}\)是摄像机的光心在世界坐标系下的坐标；\(\mathbf{d}\)是直线方向，是世界坐标系下的一个单位向量；\(t\)是一个实数，表示从\(\mathbf{o}\)沿着视线方向的距离。任意给定一个\(t\)，我们就可以得到一个点的位置。

我们说体渲染是视线\(r(t)\)上所有的点投射到图像上形成像素颜色\(C\)的过程，具体公式如下： \[ C(\mathbf{r}) = \int_{t_n}^{t_f}T(t)\sigma(\mathbf{r}(t))\mathbf{c}(\mathbf{r}(t),\mathbf{d})dt,\quad where \ T(t) = \exp (-\int _{t_n}^{t} \sigma(\mathbf{r}(s))ds) \] 其中，\(\mathbf{r}(t)\)是三维空间中的一个点，\(\mathbf{d}\)是视线的方向，三维场景的近端和远端边界分别为\(t_n\)和\(t_f\)，\(\mathbf{c}(\mathbf{r}(t), \mathbf{d})\)表示三维点\(\mathbf{r}(t)\)从\(\mathbf{d}\)这个方向上看到的颜色值，\(\sigma(\mathbf{r}(t))\)是体密度函数，\(T(t)\)是射线上从\(t_n\)到\(t\)的累积透射率。

关于体渲染的实际物理含义说明，可以参考NeRF介绍+体渲染+神经网络+源码链接+UE实践一条龙 bilibili。真实建模过程涉及到概率的知识。

在实际的计算机实现中，需要用离散来模拟积分的过程。通过在射线上进行点的采样，得到\(t_1, t_2, ..., t_N\)等多个采样点，然后进行离散化计算。最终的离散化体渲染公式如下： \[ C(r) = \sum_{i=1}^{N} T_i(1-\exp(-\sigma_i \delta_i))\mathbf{c}_i, \quad where \ T_i = \exp(-\sum_{j=1}^{i-1}\sigma_j\delta_j) \] 其中，\(\delta_i = t_{i+1} - t_i\)，表示相邻采样点之间的距离。

在NeRF中，使用分层抽样的方式来进行采样。具体来说，将\([t_n, t_f]\)拆分为\(N\)个均匀分布空间，然后从每个区间中随机均匀抽取一个样本\(t_i\): \[ t_i \sim \mathcal{U}[t_n + \frac{i-1}{N}(t_f-t_n), t_n + \frac{i}{N}(t_f - t_n)], \quad i:1\rightarrow N \] 我们可以简单总结一下体渲染的作用。

考虑眼睛和像素之间形成的射线，体渲染完成的就是射线r上所有的点投射到该图像像素上形成颜色C的过程。

原始的体渲染是积分的方式，在计算机实现中需要使用离散的表示，则引入了采样策略。

总结来说，体渲染是这样一个过程。我们首先有一个射线，通过某种采样策略可以得到\(N\)个点，对于每个点，我们都可以得到该点的不透明度\(\sigma\)以及该点在射线对应方向上的颜色\(c\)，然后通过上面提到的离散化公式，就可以计算出射线与图像平面相交所对应像素的颜色。

简单总结

NeRF提出了一种场景的隐式表达方式，利用神经辐射场来表示3维场景，是该类工作的开山之作。它结合了计算机图形学和深度学习中两个比较简单的概念，即神经网络和体渲染，但是取得了很好的效果。

NeRF的项目地址：

原始项目：bmild/nerf: Code release for NeRF (Neural Radiance Fields)
Pytorch实现：yenchenlin/nerf-pytorch
Pytorch Lightning实现：kwea123/nerf_pl

PixelNeRF(CVPR2021)

原始的NeRF存在一些问题：

不具备泛化性，对于每个单独场景都需要重新训练一个MLP
对于稀疏视图的处理比较糟糕，在可用训练图像数据不足的情况下，渲染出来的新视角效果不佳

PixelNeRF(CVPR2021)针对这两个问题进行优化。原始的NeRF在网络中并没有使用图像信息，图像只被用来做最后的监督；PixelNeRF则将图像本身也融入网络的输入去构建NeRF MLP。同时经过大量不同场景的训练之后，PixelNeRF能够表现出泛化性，仅通过输入一张(或者多张)视图，就能够重建出较好的神经辐射场。

模型架构

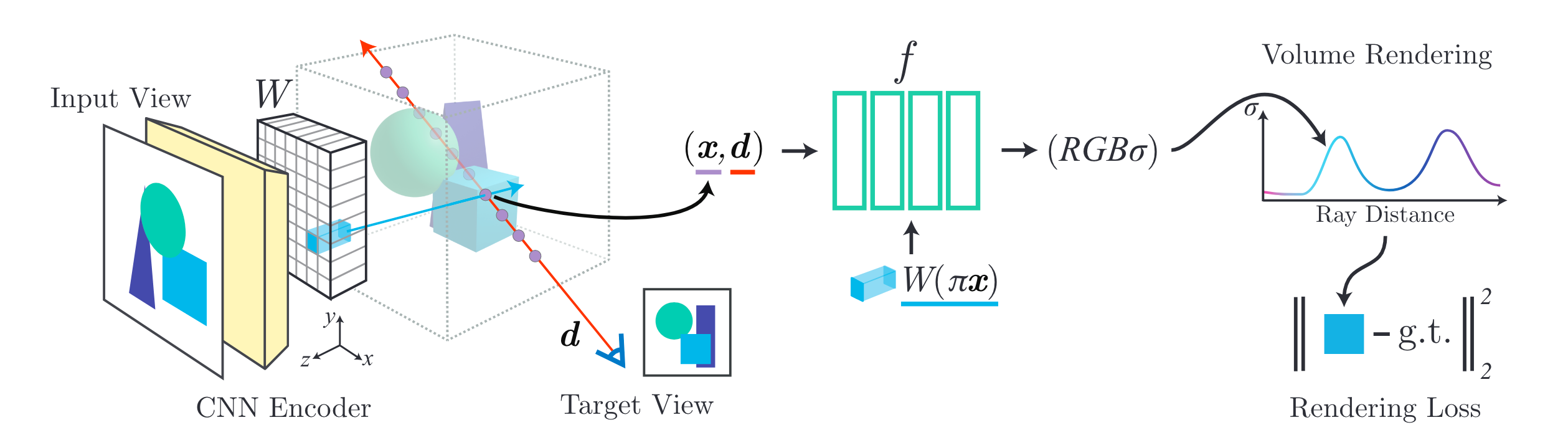
首先介绍在单张图像输入情况下的PixelNeRF。其中需要指明的一点是，这里使用的坐标系统都是输入图像对应的相机坐标系。

首先，PixelNeRF使用一个CNN Encoder对图像进行特征抽取，得到\(\mathbf{W} = E(\mathbf{I})\)，这些特征是后续输入NeRF MLP的基础
原始的NeRF MLP，输入是位置坐标和视角方向对应的位置编码，PixelNeRF在此基础上增加了图像特征作为输入，即\(\mathbf{W}(\pi(\mathbf{x}))\)，其中\(\pi(\mathbf{x})\)表示将坐标映射到图像坐标系中。由于图像特征\(\mathbf{W}\)都是整数坐标，\(\pi(\mathbf{x})\)进行映射之后，还需要进行双线性插值才能得到\(\mathbf{W}(\pi(\mathbf{x}))\)，此时NeRF MLP(上图中绿色网络)就可以表述如下，其中\(\gamma(*)\)表示NeRF中使用的位置编码：

\[ f(\gamma(\mathbf{x}), \mathbf{d};\mathbf{W}(\pi(\mathbf{x}))) = (\sigma, \mathbf{c}) \]

其余流程则基本与NeRF一致，在成像的时候对光线进行采样，采样得到的位置坐标\(\mathbf{x}\)和方向\(\mathbf{d}\)之后，在图像特征Volume中计算出\(\mathbf{W}(\pi(\mathbf{x}))\)，共同输入MLP网络之后得到\(RGB\sigma\)，利用体渲染公式渲染出图像，与GT作Loss进行监督

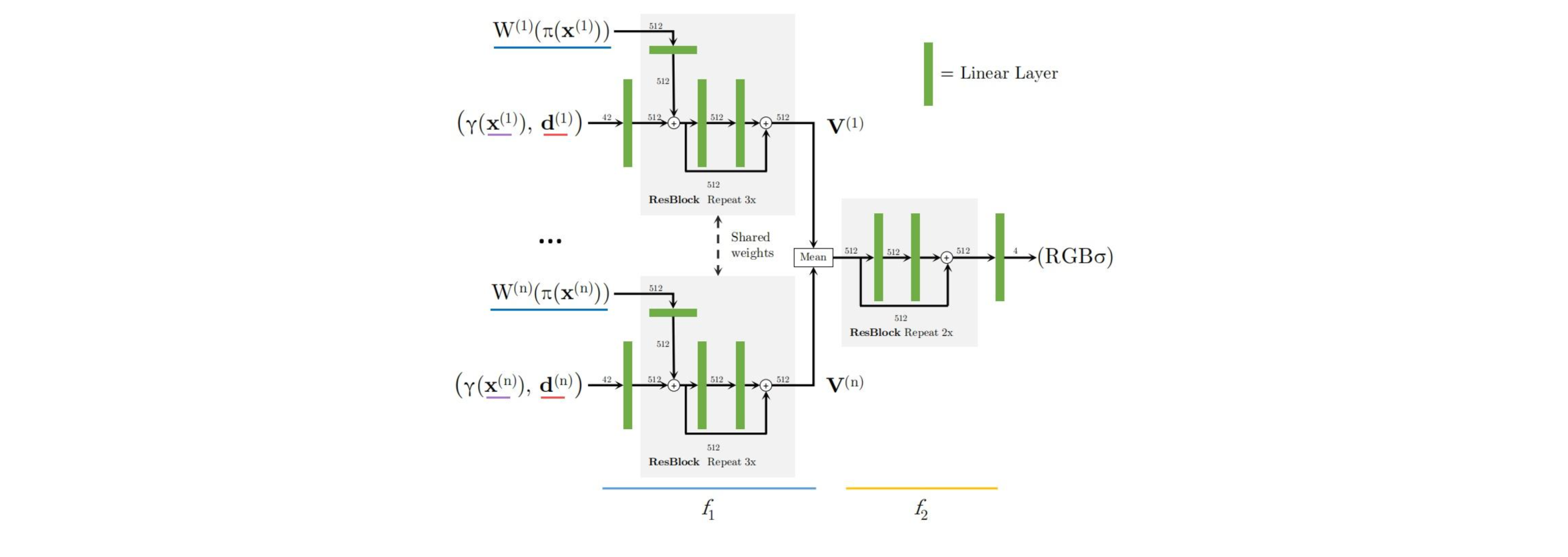
PixelNeRF同样提供多视图的版本。在多视图的情况下，假设输入的图像是\(\{\mathbf{I}^{(1)}, \mathbf{I}^{(2)}, \dots, \mathbf{I}^{(n)}\}\)。对于每个输入图像\(\mathbf{I}^{(i)}\)，都可以经过特征抽取网络得到\(\mathbf{W}^{(i)}\)。对于每个输入图像，我们都在其对应的相机坐标系下进行处理，将采样得到的世界坐标\(\mathbf{x}\)映射到相应相机坐标系下得到\(\mathbf{x}^{i}\)。这样就可以将\(\gamma(\mathbf{x}^{i}), \mathbf{d}^{(i)}, \mathbf{W}^{i}(\pi(\mathbf{x}^{(i)}))\)输入网络。我们可以将NeRF MLP看作两部分\(f_1, f_2\)。每张图片对应的\(\gamma(\mathbf{x}^{i}), \mathbf{d}^{(i)}, \mathbf{W}^{i}(\pi(\mathbf{x}^{(i)}))\)输入共享权重的\(f_1\)之后，得到\(\mathbf{V}^{(i)}\)。所有的\(\mathbf{V}^{(i)}\)经过平均池化之后，经过后续的\(f_2\)得到输出\(RGB\sigma\)。

简单总结

PixelNeRF在原始NeRF的基础上，在输入中增加了图像特征。PixelNeRF在大量训练过后，能够表现出泛化性，并且在稀疏视图的情况下，也能有较好的表现。

PixelNeRF的项目地址：sxyu/pixel-nerf: PixelNeRF Official Repository

MipNeRF(ICCV2021)

原始的NeRF在对每个像素进行成像的时候，会从光心向像素投射一条光线。这种方式导致NeRF在处理一些多尺度图像的时候，会得到不好的效果。具体来说，如果NeRF在低分辨率图像情况下进行学习，最终得到的结果会出现锯齿现象；如果NeRF在给定的一系列多种不同分辨率的混合图像下进行学习，最终得到的结果在近景中表现为模糊，在远景中表现为锯齿。一种最直接的解决方式就是在每个像素成像的时候，投射多条光线，但是这会导致性能消耗成倍增加，是一种不现实的方式。

而MipNeRF(ICCV2021)则选择了一种圆锥体投影的方式来改进原始NeRF对于每个像素成像的过程。简单来说，MipNeRF在对每个像素进行成像的时候，向该方向上投影出一个圆锥体，然后考虑不同的圆锥台来进行成像。

模型架构

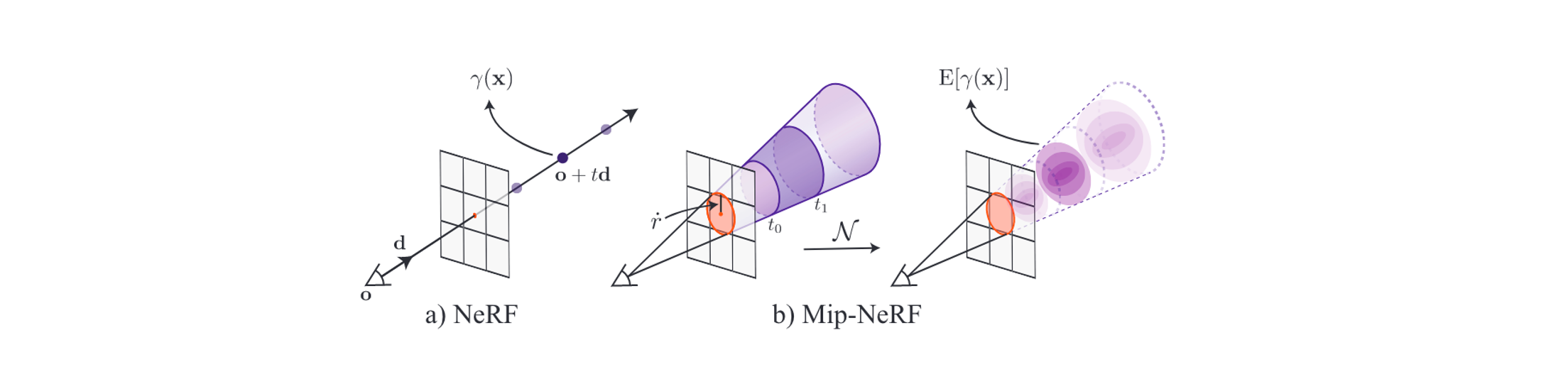
我们首先关注MipNeRF对于一个像素成像的过程。对于某个像素，我们可以如上图所示投射出一个圆锥体，然后通过在中心射线上进行采样得到\(t_0, t_1, ...,t_N\)，这些采样点可以将投射圆锥体分割成多个圆锥台。对于每个圆锥台，我们希望求出它平均的颜色和体密度，对比NeRF就相当于得到了每个采样点的颜色和体密度，然后按照离散的体渲染公式就可以得到该像素的颜色。

那么接下来要解决的问题就是如何求出每个圆锥台的平均颜色和体密度。像NeRF一样，Mip-NeRF同样考虑使用神经网络来建模，因此我们目前有的是一个神经网络，它输入编码过后的空间位置和观察方向，输出对应的体密度\(\sigma\)和方向相关的颜色\(c\)。

对于给定的\(t_{i},t_{i+1}, \mathbf{o}, \mathbf{d}\)，我们可以判断某个位置\(\mathbf{x}\)是否在圆锥台内，如下所示： \[ F(\mathbf{x}, \mathbf{o}, \mathbf{d}, \dot{r},t_0, t_1) = \mathbb{I}[{t_0 < \frac{\mathbf{d}^T(\mathbf{x} - \mathbf{o})}{||\mathbf{d}||_2^2} < t_1) \wedge (\frac{\mathbf{d}^T(\mathbf{x} - \mathbf{o})}{||\mathbf{d}||_2 ||\mathbf{x} - \mathbf{o}||_2} > \frac{1}{\sqrt{1 + (\dot{r} / ||\mathbf{d}_2||)^2}}]} \] 圆锥台的平均颜色和体密度，实际上就可以通过求得圆锥台内每个点的颜色和体密度，再进行平均即可。虽然我们可以像NeRF那样处理每个点得到输出，但是显然并不现实，这会带来大量的性能消耗。回顾NeRF的神经网络，它接收经过位置编码过后的空间位置和观察方向得到该点的颜色和体密度；而Mip-NeRF中使用的神经网络，接收的是某个圆锥台对应的特征，输出该圆锥台的平均颜色和体密度。

Mip-NeRF中，圆锥台对应的特征，实际上是圆锥台内所有点位置编码的期望。假设对于每个空间位置\(\mathbf{x}\)，对应的位置编码为\(\gamma(\mathbf{x})\)，那么所有点位置编码的期望计算如下： \[ \gamma^*(\mathbf{o}, \mathbf{d}, \dot{r},t_0, t_1) = \frac{\int \gamma(\mathbf{x})F(\mathbf{x}, \mathbf{o}, \mathbf{d}, \dot{r},t_0, t_1) d\mathbf{x}}{\int F(\mathbf{x}, \mathbf{o}, \mathbf{d}, \dot{r},t_0, t_1)d\mathbf{x}} \] 上面的期望并没有封闭形式可供使用，于是MipNeRF使用3D Gaussian来近似圆锥台，这样可以有效地近似获取所需特征（下面的一系列操作都是为了近似得到上面期望计算的封闭形式），这被MipNeRF称为集成位置编码(Integrated Positional Encoding,IPE)。3D Gaussian所需的参数\(\mathbf{\mu},\Sigma\)，可以通过公式计算出来，这里不进行推导，假设我们已经有了这些参数。于是需要计算的IPE就是\(\gamma(\mu, \Sigma)\)。

对于NeRF的位置编码\(\gamma(q) = (\sin(2^0\pi q), \cos(2^0\pi q), \dots, \sin(2^{L-1}\pi q), \cos (2^{L-1}\pi q))\)，可以写成矩阵的形式： \[ \begin{aligned} P &= \begin{bmatrix} 1 & 0 & 0 & 2 & 0 & 0 & ... & 2^{L-1} & 0 & 0 \\ 0 & 1 & 0 & 0 & 2 & 0 & ... & 0 & 2^{L-1} & 0 \\ 0 & 0 & 1 & 0 & 0 & 2 & ... & 0 & 0 & 2^{L-1} \\ \end{bmatrix} \\ \gamma(\mathbf{x}) &= \begin{bmatrix} \sin P\mathbf{x} \\ \cos P\mathbf{x} \end{bmatrix} \end{aligned} \] 在3D Gaussian近似的情况下，\(\mathbf{x}\)服从高斯分布，进行线性变换之后，\(P\mathbf{x}\)也服从高斯分布，对应的均值\(\mu_\gamma\)和方差\(\Sigma_\gamma\)分别为： \[ \mu_\gamma = P\mu , \quad \Sigma_\gamma = P\Sigma P^T \] 同时在高斯分布下，我们有sin和cos的期望： \[ \begin{aligned} E_{p\sim \mathcal{N}(\mu, \sigma^2)}[\sin(p)] &= \sin(\mu)\exp (-\frac{1}{2} \sigma^2) \\ E_{p\sim \mathcal{N}(\mu, \sigma^2)}[\cos(p)] &= \cos(\mu)\exp (-\frac{1}{2} \sigma^2) \end{aligned} \] 所以在3D Gaussian近似的情况下，位置编码的期望，或者说是IPE，\(\gamma(\mu, \Sigma)\)的计算公式如下： \[ \gamma(\mu, \Sigma) = E_{\mathbf{x}\sim \mathcal{N}(\mu_\gamma, \Sigma_\gamma)}[\gamma(\mathbf{x})] = \begin{bmatrix} \sin(\mu_\gamma) \circ \exp(-1/2\ \text{diag}{(\Sigma_\gamma}) )\\ \cos(\mu_\gamma) \circ \exp(-1/2\ \text{diag}{(\Sigma_\gamma})) \end{bmatrix} \] 其中，\(\mu\)和\(\Sigma\)是原始的3D Gaussian近似，\(\mu_\gamma, \Sigma_\gamma\)是经过位置编码之后的高斯分布参数；\(\circ\)表示按元素乘法；\(\text{diag}\)表示取对角线元素。并且由于完整的矩阵太大，我们这里直接通过下面的方式计算对角线元素： \[ \begin{aligned} \text{diag}(\Sigma_\gamma) &= [\text{diag}(\Sigma),4\text{diag}(\Sigma),\dots, 4^{L-1}\text{diag}(\Sigma)]^T \\ \text{diag}(\Sigma) &= \sigma_t^2(\mathbf{d} \circ \mathbf{d}) + \sigma_r^2(\mathbf{1} - \frac{\mathbf{d} \circ \mathbf{d}}{||\mathbf{d}||_2^2}) \end{aligned} \] 至此，我们就得到了每个圆锥台的特征表示。将这个特征表示送入神经网络，得到对应的平均颜色和体密度的输出，就可以按照与NeRF相同的流程进行训练和渲染了。

MipNeRF通过对IPE和普通位置编码PE进行单维度的可视化发现，IPE保留在某个t间隔内恒定的频率，并且轻微删除在某个t间隔内变化的频率；而PE则保留所有频率

这里还有一些细节需要注意，MipNeRF同样采用与NeRF类似的coarse和fine的训练策略，不过与NeRF不同的是，MipNeRF只需要训练一个MLP即可。因为MipNeRF显示地对圆锥体的位置和大小进行编码，引入了尺度信息，因此可以对多尺度的场景进行建模。在coarse和fine的训练策略中，则仍然使用分层抽样和重要性抽样的抽样策略。不过MipNeRF在重要性抽样之前，对\(w\)进行了一些小改动，然后再进行归一化。和式的前半部分是为了让重要性函数更加平滑，后半部分的常数\(\alpha\)则是为了能够在空白区域也进行采样。 \[ w'_k = \frac{1}{2} (\max(w_{k-1},w_k) + \max(w_k, w_{k+1})) + \alpha \] NeRF和MipNeRF的主要区别在于对单个像素的成像过程：

NeRF向单个像素投射出一条光线，在光线上采样多个点，然后将点的位置以及方向进行位置编码得到特征，输入MLP，得到该点的颜色和体密度，然后利用离散的体渲染得到像素颜色
MipNeRF向单个像素投射出一个圆锥体，在圆锥体中心射线上进行采样，将圆锥体切分成多个圆锥台。对于每个圆锥台，通过近似模拟计算出集成位置编码以及方向的位置编码，输入MLP之后得到该圆锥台的平均颜色和体密度，同样利用离散的体渲染得到像素颜色

简单总结

MipNeRF最终可以在训练和测试期间高效渲染出抗锯齿的图像，并且允许我们在训练期间使用多尺度的图片。MipNeRF通过向单个像素投射圆锥体的方式，将Volume的大小和形状特征引入网络，使得网络能够学习到多尺度的特征。并且相比于NeRF训练两个MLP，MipNeRF只需要训练单独一个MLP即可。

MipNeRF项目地址：

原始项目：google/mipnerf
Pytorch Lightning实现：hjxwhy/mipnerf_pl

MipNeRF-360(CVPR2022)

MipNeRF-360主要解决的问题是对无界场景(unbounded scene)。这种无界场景与llff数据集这种forward scene前向场景有所不同，llff的forward scene可以通过NDC空间变换成有界的，这种变换可以通过沿着z轴进行视图变换、投影变换等完成。而无界场景除了没有边界，它的相机视角也是任意的，因此无法使用NDC空间转换成有界。

NDC，Normalized Device Coordinates，归一化设备坐标。指的是一种坐标系统。

在三维图形渲染的过程中，物体的坐标首先在世界坐标系中被定义，然后通过一系列变换（视图变换、投影变换等）转换到一个特定的范围内，通常是一个立方体空间，其中每个轴的取值范围是[-1, 1]。这个过程中产生的坐标就是归一化设备坐标。这种做法的好处是可以简化不同设备之间图形渲染过程，适配各种不同的分辨率和屏幕尺寸。通过这种方式，图形系统可以轻松地将图像从一个标准化的空间映射到实际的现实设备上。

对于无界场景的处理，NeRF类模型通常会存在以下问题：

第一个是3D坐标的Parameterization参数化问题(如何表示3D坐标)。NeRF类模型处理的都是有界场景，即需要知道near和far。例如对于合成数据集nerf_synthetic，场景中只有某个物体，而没有背景，NeRF直接使用世界坐标系作为3D坐标的参数化；对于真实场景数据集llff，这种forward scene前向场景，NeRF使用NDC空间将其变换成有界的。而对于无界场景(各种方向)，我们无法使用NDC空间进行转换。因此我们希望能够得到一种3D坐标参数化方法，使得NeRF类模型能够将无界场景处理为有界的，从而进行后续工作。同时，理想的3D场景参数化应该做到为附近的内容分配更多的容量，为远处的内容分配更少的容量。

第二个是Efficiency效率。无界场景通常也对应大型而详细的场景，更大的场景就意味着更大的MLP，并且在训练过程中，渲染需要多次查询大型MLP，这种成本是非常昂贵的。另一方面，NeRF在训练过程中，还存在coarse和fine两个训练阶段，这又导致效率的进一步下降。

第三个是Ambiguity模糊性。在无界场景中，背景区域明显比中心区域的光线系数，这种现象加剧了3D重建出结果的模糊性。对于没有在训练样本中出现的新视角，NeRF重建很有可能出现模糊或者伪影。

针对这三个问题，MipNeRF-360(CVPR2022)进行了对应的改进，分别是non-linear scene parameterization(非线性场景参数化)、online distillation(在线蒸馏)和distortion-based regularizer(基于失真的正则化)。

模型架构

non-linear scene parameterization

对于第一个Parameterization问题，MipNeRF-360使用非线性场景参数化来解决。

MipNeRF使用高斯分布的\(\mu,\Sigma\)来表示每个圆锥台，最终输入MLP的特征是\(\gamma(\mu, \Sigma)\)。接下来，假设我们使用一个非线性函数\(f(\mathbf{x})\)来重参数化这个高斯分布，那么重参数化之后的高斯分布对应参数计算如下： \[ \begin{aligned} &对f(\mathbf{x})在\mu进行泰勒展开，f(x) \approx f(\mu) + \mathbf{J}_f(\mu)(\mathbf{x} - \mu), 其中\mathbf{J}_f(\mu)是f(\mathbf{x})在\mu处的Jacobian行列式 \\ & 将f(\mathbf{x})作用在高斯上，则有f(\mu, \Sigma) = (f(\mu), \mathbf{J}_f(\mu)\Sigma \mathbf{J}_f(\mu)^T)\\ & 其中\mathbf{J}_f(\mu) = \frac{\partial f}{\partial \mu}, \mathbf{J}_f(\mu)\Sigma \mathbf{J}_f(\mu)^T = (\mathbf{J}_f(\mu)(\mathbf{J}_f(\mu)\Sigma)^T)^T \end{aligned} \] 对于任意一个非线性函数\(f(\mathbf{x})\)，我们都可以利用上面的方式计算出重参数化之后的高斯分布。这里MipNeRF-360使用的非线性函数如下： \[ f(\mathbf{x}) = \text{contract}(\mathbf{x}) = \left\{\begin{matrix} \mathbf{x} & ||\mathbf{x}|| \le 1 \\ (2 - \frac{1}{||\mathbf{x}||}) (\frac{\mathbf{x}}{||\mathbf{x}||})& ||\mathbf{x}|| > 1 \end{matrix}\right. \] 这种线性函数与NDC空间有相似的指导思想，即远处的点按照距离反比进行分布。

下面这张图可视化了重参数化前后的高斯分布变化：

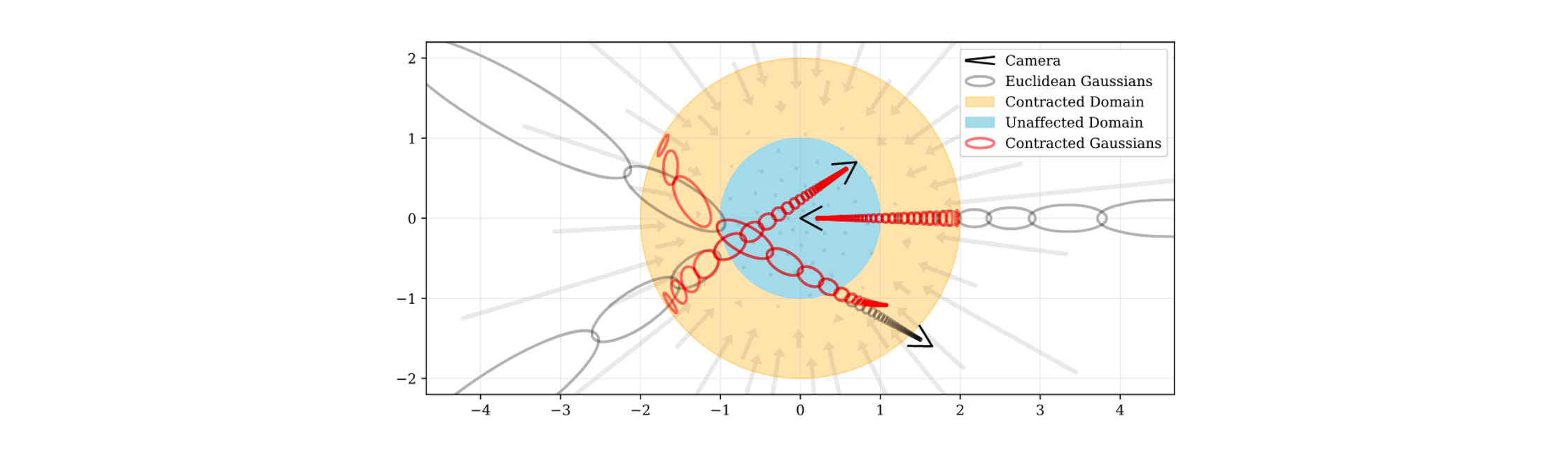
灰色的高斯表示在重参数化之前分布，红色高斯表示经过contract重参数化之后的分布。可以看到，这种重参数化使得所有的高斯都收缩在一个半径为2的球内，这样无界场景就收缩到有界范围内了。在这个球内，蓝色区域表示高斯不受影响，黄色区域表示高斯被收缩了。

解决了3D坐标的参数化，采样方式也需要进行设计。原始的NeRF使用均匀分层采样。对于欧式空间，均匀分层采样对应的实际物理含义是按照真实深度均匀采样；对于NDC空间，均匀分层采样对应的实际物理含义是按照真实的逆深度(深度的倒数)均匀采样。这种设计方式对于前向场景是非常好的，因为它可以做到在近处采样更多的点，在远处采样更少的点。但是对于无界场景却不太适用。针对这个问题，MipNeRF-360设计了一种按照逆深度进行线性采样的方式。

首先，定义归一化光线距离\(s\)，定义如下： \[ s = \frac{g(t) - g(t_n)}{g(t_f) - g(t_n)}, \quad t = g^{-1}(s\cdot g(t_f) + (1-s)\cdot g(t_n)) \] 其中\(g(*)\)是一个可逆的表量函数，左式给出了归一化光线距离\(s\)的定义，并且有\(s \in [0,1]\)；右式则给出了\(t\)和\(s\)之间的转换关系。最终MipNeRF-360使用\(g(x) = 1/x\)，并且后续统一使用光线距离\(s\)，在\(s\)距离上进行均匀采样，这样在\(t\)距离上就是按照逆深度进行均匀采样。

online distillation

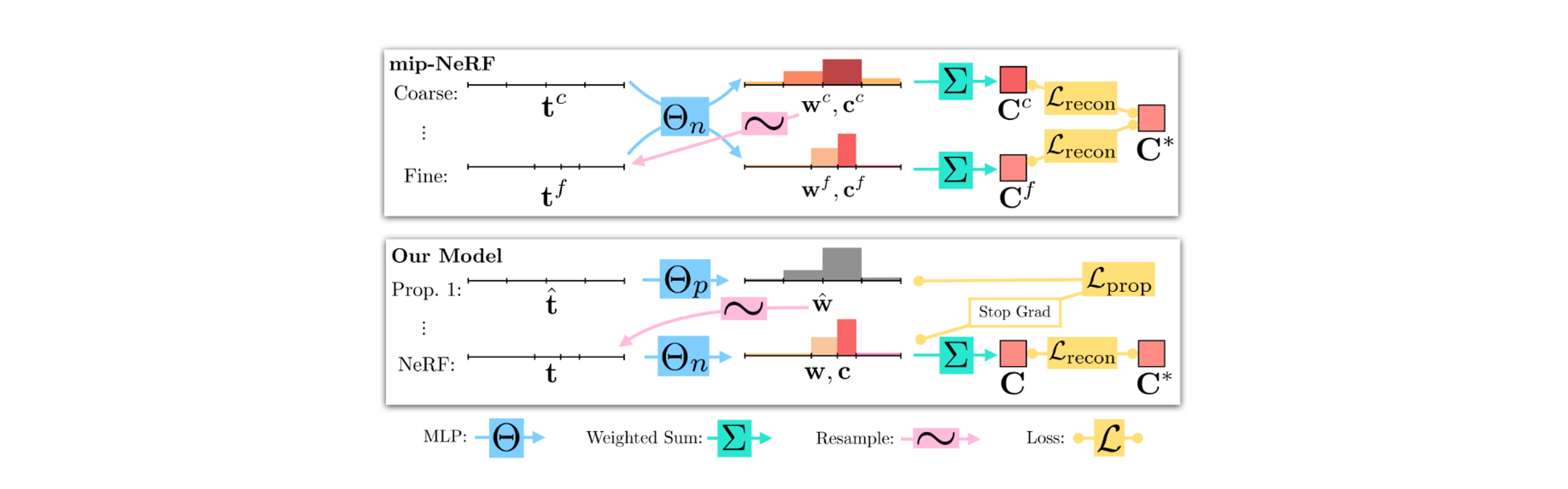
对于第二个性能问题，MipNeRF-360通过在线蒸馏的方式来解决。

在MipNeRF中，训练过程是coarse to fine的。简单来说，首先通过均匀采样进行一次Coarse流程，该流程会得到一个重要性分布直方图，根据这个直方图进行重要性采样，然后进行一次fine流程。论文认为，Coarse流程中后半段预测颜色并使用原图监督的过程是没有必要的，因为我们只希望Coarse流程得到重要性分布直方图即可。于是MipNeRF-360将这个流程改进为两步，首先均匀采样通过一个Proposal MLP，该网络直接输出一个重要性直方图，然后再根据这个直方图进行重要性采样，经过下面的NeRF MLP，该网络的流程与Fine MipNeRF完全相同。

由于Proposal MLP不需要预测颜色，因此它的大小会比NeRF MLP小很多，所以MipNeRF-360能够做到在容量更高的同时，训练成本不会增加很多。

在这种训练策略下，随之而来出现的问题是如何监督Proposal网络。Proposal MLP会得到一个直方图，NeRF MLP同样会得到一个直方图。我们可能很直接的想到可以用更精细的NeRF Net重要性直方图去监督Proposal MLP直方图，但是这是不对的。因为在这种情况下，我们并不是想让两个直方图相同，而是希望两个直方图能够代表同样的分布。为此，MipNeRF-360设计了特殊的损失函数，来鼓励两个具有不同区间划分的直方图一致(代表同样的分布)。这个损失函数应当有这样的特点，即当两个直方图对应不同的分布时，损失值大于0；否则损失值等于0。

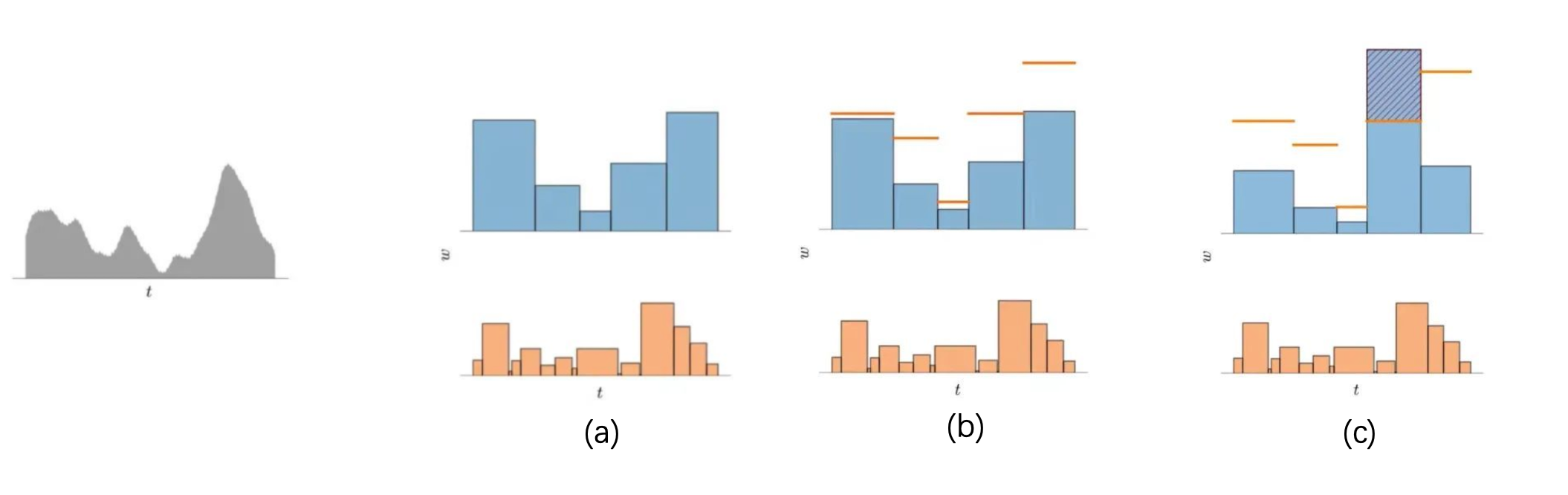
考虑上面的第一幅图是真实分布，我们可能得到(a)这样的两个直方图。MipNeRF-360认为，如果两个直方图刻画同一个分布，那么在重叠区间内，其中一个直方图的权重一定不会超过另一个直方图重叠区间权重总和。根据这个假定，我们就可以利用其中一个直方图来给构造另一个直方图的上限。方式如下： \[ \text{bound}(\hat{\mathbf{t}},\hat{\mathbf{w}}, T) = \sum_{j: T\cap \hat{T}_j \neq \varnothing} \hat{w}_j \] 其中\(\hat{\mathbf{t}},\hat{\mathbf{w}}\)表示Proposal MLP输出的直方图，\(T\)表示给定的间隔。如果NeRF MLP对应直方图\(\mathbf{t},\mathbf{w}\)与Proposal MLP输出直方图对应同一分布，那么则需要满足在每个对应区间内，都有\(w_i \le \text{bound}(\hat{\mathbf{t}},\hat{\mathbf{w}}, T_i)\)，如上图(b)所示。而损失函数就可以用下面这种方式设计，用来惩罚超过边界范围的直方图值。 \[ \mathcal{L}_{prop}(\mathbf{t},\mathbf{w},\hat{\mathbf{t}},\hat{\mathbf{w}}) = \sum_i \frac{1}{w_i} \max(0, w_i - \text{bound}(\hat{\mathbf{t}},\hat{\mathbf{w}}, T_i))^2 \] 可以看出，MipNeRF选择使用Proposal MLP输出的直方图，去构造NeRF MLP直方图的上限，由此来计算损失。这种损失是不对称的，它会指导Proposal MLP去弥补那些评估不足的地方(underestimate)，而过度评估的地方(overestimate)则认为可以接受。

distortion-based regularizer

针对第三个模糊问题，MipNeRF-360使用了基于失真的正则化来解决。

传统的NeRF经过训练之后会表现出两种模糊现象：

“floaters”：指的是在体积密度空间中小的不相连的区域，这些区域被渲染之后可能对某些视角的渲染结果有帮助，但是在其他视角下观察就像一些漂浮物
“background collapse”：远处的表面被错误地建模成靠近相机的密集内容的半透明云

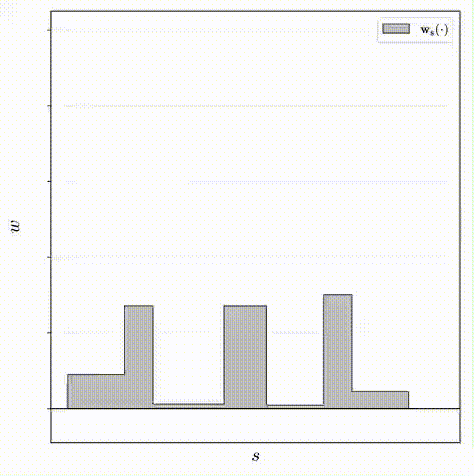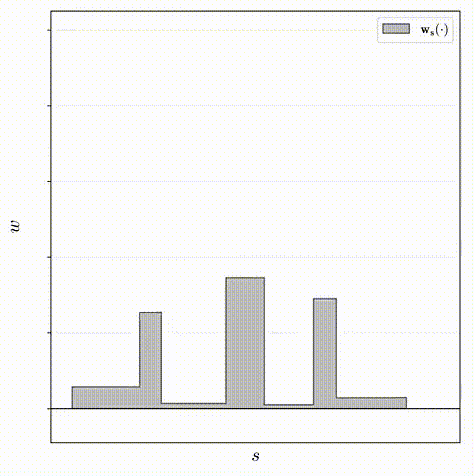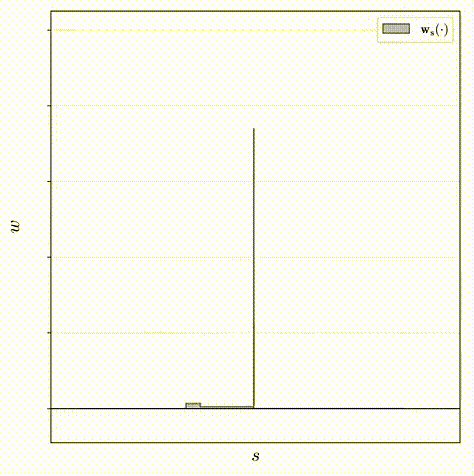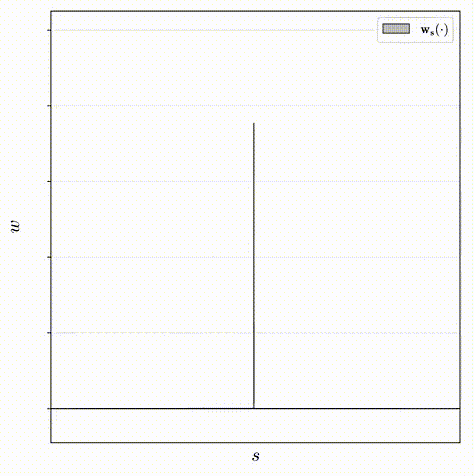
MipNeRF-360则在重要性分布上进行优化，提出了一个基于失真的正则化器。这里使用上面提到的归一化光线距离，计算方式如下： \[ \mathcal{L}_{dist}(\mathbf{s}, \mathbf{w}) = \iint_{-\infty}^{\infty} \mathbf{w}_s(u)\mathbf{w}_s(v) |u-v| du dv \] 其中\(\mathbf{w}_s(u)\)的值是通过对\((\mathbf{s},\mathbf{w})\)定义的阶跃函数插值得来的。这个正则化器计算的是所有点对之间的距离，并使用\(w\)作为权重，实际上是为了最小化直方图的面积，迫使\(\mathbf{s}, \mathbf{w}\)形成一个单峰的直方图。当然上面的公式并不容易计算，离散化后的表达如下： \[ \mathcal{L}_{dist}(\mathbf{s}, \mathbf{w}) = \sum_{i,j} w_i w_j | \frac{s_i + s_{i+1}}{2} - \frac{s_j+s_{j+1}}{2}| + \frac{1}{3} \sum_i w_i^2(s_{i+1} - s_{i}) \] 基于失真的优化器