3D Gaussian介绍以及综述

Introduction

资源列表

3D Gaussian相关跟踪项目：

3D Gaussian综述以及相关项目：

3D Gaussian Splatting

3D Gaussian Splatting(SIGGRAPH2023)提出了一种新的场景表达方式，它使用3D Gaussian当作场景基元，利用众多3D Gaussian来表示场景。在训练过程中通过对3D Gaussian进行交错优化和致密化，以实现场景的准确表示。在渲染方面，开发了一种支持3D Gaussian的可微光栅化器。

3D Gaussian Splatting能够在较少训练时间的情况下同时保持优秀的渲染质量，最重要的是允许在1080p分辨率下进行高质量实时(\(\ge\) 30 fps)的新视图合成。

模型架构

3D Gaussian Splatting的总体流程如下，这里可以进行简单描述。首先，通过SfM来处理场景的多张图片，输出初始点云。将点云中的每个点作为中心点，将其初始化为3D Gaussian，每个3D Gaussian还具有其他可优化的参数。给定一个视角，我们可以将3D Gaussian投影到2D，通过球谐函数得到相应的颜色，然后进行\(\alpha\)混合得到渲染结果，该过程通过论文设计的可微分光栅化器来完成。得到渲染结果之后，可以与GT作Loss，而后进行反向传播。反向传播的梯度一方面用来优化3D Gaussian的各项参数，另一方面用来完成3D Gaussian的致密化。

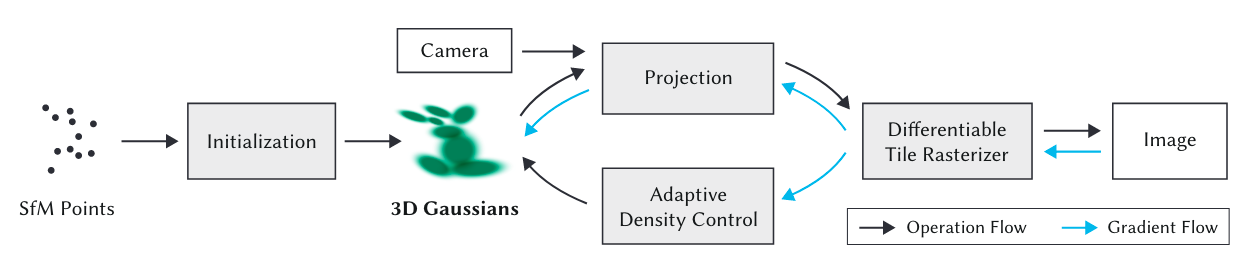
上面简单介绍了模型的全流程，下面对其中的不同组件进行介绍。

3D Gaussian 基元

论文中使用3D Gaussian作为场景基元，每个3D Gaussian的可优化参数包括位置position(对应Gaussian的均值)\(\mathbf{x}\)，协方差矩阵Covariance\(\Sigma\)，不透明度Opacity \(\alpha\)，以及球谐函数SH系数(用来表示视角相关的颜色)。3D Gaussian表示如下。直观上来看，每个3D Gaussian都表现为一个具有不透明度的椭球，同时具有不同的缩放和旋转。 \[ G(\mathbf{x}) = e ^{-\frac{1}{2}(\mathbf{x})^T \Sigma^{-1}(\mathbf{x})} \] 3D Gaussian中的大部分参数都可以直接通过梯度下降来进行优化，不过其中需要注意的是，协方差矩阵只有在半正定的时候才有意义。如果直接使用梯度下降来优化这样的矩阵是非常困难的，因为我们很难直接在优化过程中给矩阵增加这样的约束，这导致过程中产生的矩阵可能是无效的。为此，论文将\(\Sigma\)分解为旋转和缩放的组合，允许独立优化旋转和缩放，使得3D Gaussian适应场景中的不同形状： \[ \Sigma = RSS^TR^T \] 其中，\(S\)是一个对角缩放矩阵，其中包含\(3\)个缩放参数；\(R\)是一个\(3\times 3\)旋转矩阵。在实际实现中，为了允许对这两个因子独立优化，选择将其分别存储，其中利用一个3维向量\(s \in \mathbb{R}^3\)来存储\(S\)，利用4元数\(q \in \mathbb{R}^4\)来表示\(R\)，利用\(s,q\)可以分别导出\(S,Q\)。

4元数提供了一种有效的方法，来处理三维空间旋转和定位问题。与欧拉角相比，四元数避免了万向锁问题，并且在计算上比旋转矩阵更高效、更紧凑。通过四元数可以实现平滑的插值和连续的旋转。

4元数认为三维空间中的旋转可以通过一个实部和三个虚部来定义，形式上为\(q = w + xi + yj + zk\)。在旋转中，实部\(w\)表示旋转的角度，而虚部\((x,y,z)\)表示旋转轴的方向。详细理解可以参考：四元数如何控制物体旋转？ bilibili

自适应致密化

从初始化开始，我们只有经过SfM得到的一些初始化点，在后续的流程中，3D Gaussian Splatting会自适应地增加高斯密度，以更好地捕捉场景细节，即自适应致密化。具体来说，它会在重建不足的区域进行Gaussian的克隆，在过度重建的区域进行Gaussian的分裂。这两者在反向传播过程中都表现出较大的空间位置梯度。对于重建不足的小Gaussian，会沿着梯度方向创建出相同大小的小Gaussian；对于过度重建的大Gaussian，会将其分割成更小的Gaussian，大小除以某个尺度因子\(\phi(=1.6)\)。

以上致密化的过程会周期性进行(在预热之后，每100次迭代进行一次致密化)，同时在致密化过程中会删除几乎透明的Gaussian(\(\alpha\)小于某个阈值\(\varepsilon_\alpha\))。

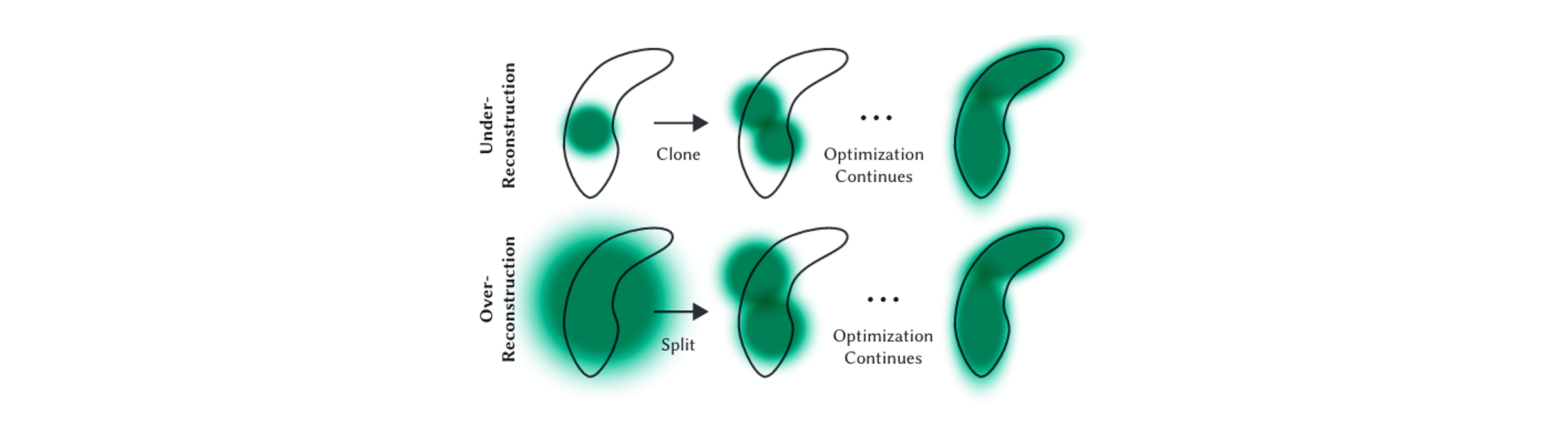
可微分光栅化

本部分介绍3D Gaussian中的可微分光栅化过程。考虑在空间中已经有很多3D Gaussian，可微分光栅化完成的工作就是在给定视角的情况下，将这些3D Gaussian转化为图像。

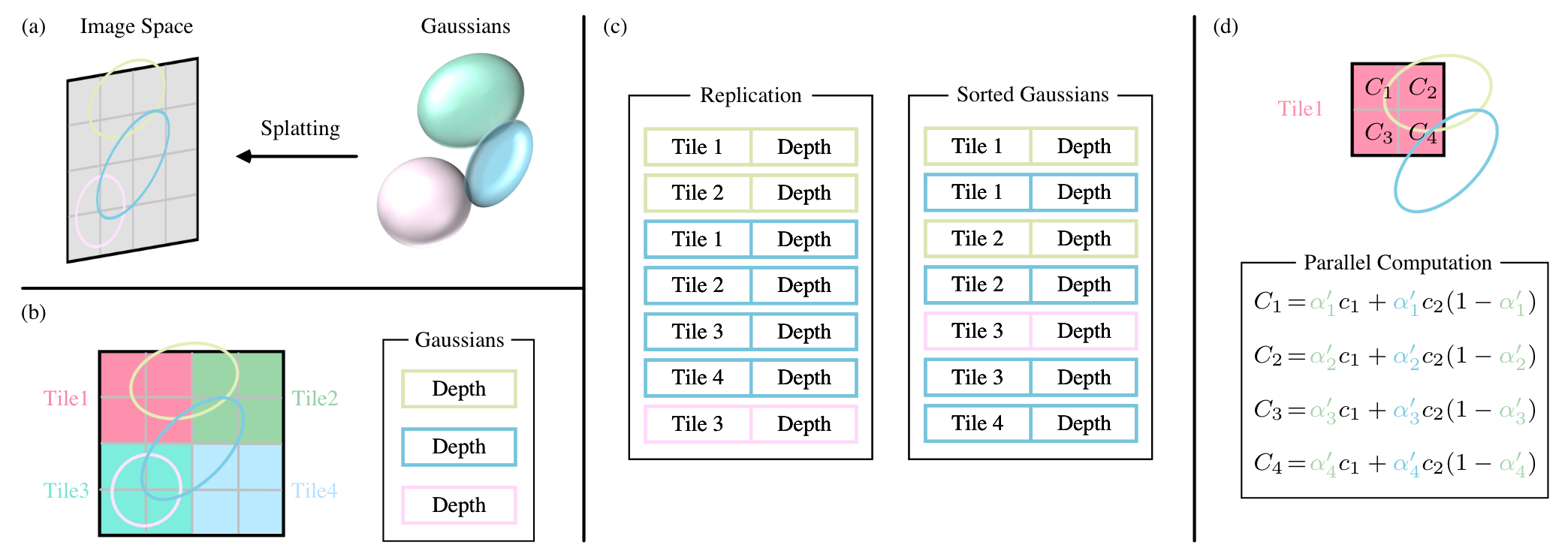
对于众多的3D Gaussian，首先需要将它们投影到2D图线空间中，形成多个2D Gaussian，这个步骤被称为Splatting。对于每个3D Gaussian，设其中心点为\(\mathbf{x}\)，协方差矩阵为\(\Sigma\)，在给定观察变换\(W\)的情况下，我们可以得到对应2D Gaussian的位置\(\mathbf{x}'\)以及协方差矩阵\(\Sigma'\)。协方差矩阵\(\Sigma'\)计算如下，其中\(J\)为投影变换的仿射近似雅可比矩阵： \[ \Sigma' = JW\Sigma W^T J^T \] 接下来首先考虑对单个像素pixel的成像过程。对于每个像素\(x\)来说，我们可以得到覆盖在它上面的所有2D Gaussian，这些2D Gaussian可以形成一个列表\(\mathcal{N}\)，其中按照Gaussian的深度进行排序。于是，像素的颜色就可以通过下面的公式计算得来： \[ C = \sum_{i \in \mathcal{N}} c_i\alpha_i' \prod_{j=1}^{i-1}(1 - \alpha_j') \] 其中，\(c_i\)表示学习得到的Gaussian的颜色，\(\alpha_i\)表示学习得到的透明度，而\(\alpha_i'\)则是通过该透明度与高斯分布相乘得到的结果，如下，需要利用到投影空间中的坐标\(x',\mathbf{\mu}_i'\): \[ \alpha_i' = \alpha_i \times \exp(-\frac{1}{2}(x' - \mu_i')^T\Sigma_i'^{-1}(x' - \mu_i')) \] 在每个像素成像之前，我们需要得到覆盖在该像素上的所有2D Gaussian，并且还需要按照深度进行排序，而场景中的Gaussian的数量级往往非常大，可以预想到，如果进行逐像素渲染的话，排序工作会是渲染过程中的瓶颈。而3D Gaussian Splatting则进行了很多并行优化，来加速这一过程。

首先，论文将图像分为很多的patch(原论文中称为tile)，每个patch的大小为\(16 \times 16\)​ pixel。对于每个patch，首先会根据视锥体来保留相关Gaussian(具体来说，我们只保留与视锥体相交的置信区间大于99%的Gaussian)，然后我们就可以得到有哪些Gaussian覆盖了每个Patch。由于一个Gaussian可能会覆盖多个patch，因此在过程中会涉及到Gaussian的复制，生成Gaussian的副本。最终，所有的Gaussian(包含复制的Gaussian)会被分配一个patch相关的id标识符。结合patch id以及深度，就可以对每个patch对应的所有Gaussian进行深度排序。

每个Patch和像素的渲染都是独立发生的，这使得过程非常适合并行化。具体来说，3D Gaussian的项目对将该过程在GPU上进行优化，由GPU的Block来执行每个Patch的渲染，同时由Block中的每个Thread来执行每个Pixel的渲染。由于每个Block具有共享内存，这使得整个过程会非常高效。对于每个像素(每个Thread)，当透明度\(\alpha\)达到1的时候，则停止渲染。

其他细节

3D Gaussian Splatting的整体流程中，还有一些其他的细节：

  1. 损失函数使用L1 Loss和SSIM Loss：\(\mathcal{L} = (1-\lambda)\mathcal{L}_1 + \lambda \mathcal{L}_{D-SSIM}\)​
  2. 在点剪枝阶段，会去除多余的或者影响较小的Gaussian，包括几乎透明(\(\alpha\)低于指定阈值)的高斯、在空间中过大的高斯、在空间中具有较大足迹的高斯等。在某种程度上可以视为正则化过程
  3. 为了防止摄像机附近Gaussian密度的不合理增加，会周期性将Gaussian的不透明度设置为接近于零。这种方式能够控制使得必要Gaussian的密度增加，同时剔除冗余的Gaussian。有助于节省计算资源，同时确保模型中的Gaussian更加精确和有效地表示场景
  4. 在优化过程中会有一个“warm up”过程，该过程中使用较低的分辨率进行计算。具体来说，首先使用4倍小的分辨率进行优化，并且分别在迭代250次以及500次时进行两倍上采样

在代码实现中，Gaussian的的实现是基于点云完成的。点云中的每个点都存储了相关属性。其中有关球谐函数的系数，包括了属性f_dc_0,f_dc_1,f_dc_2表示RGB的0阶系数，f_rest_0~f_rest_14, f_rest_15~f_rest_29, f_rest_30~f_rest_44分别表示RGB的剩余球谐系数。

简单总结

3D Gaussian Splatting提出了一种新的场景表征方式，它使用众多3D Gaussian来表示场景，同时使用可微分光栅化来渲染图像。这种方式提供了更快的训练和渲染速度，同时能够保持优秀的渲染质量。

3D Gaussian的优点：

  • 能够生成高品质、逼真的场景
  • 可以进行快速、实时的渲染
  • 更快的训练速度

3D Gaussian的缺点：

  • 在模型优化过程中，会出现“破碎”的Gaussian，包括太大、太长、冗余等
  • 在训练过程中需要更多的显存
  • 单个场景需要更多的磁盘占用空间
  • 与现有的渲染管线不兼容

3D Gaussian Splatting的相关项目地址：

相关Survey

本部分主要记录在3D Gaussian相关Survey中提到的改进方向以及相关工作等，所参考的Survey分别是：

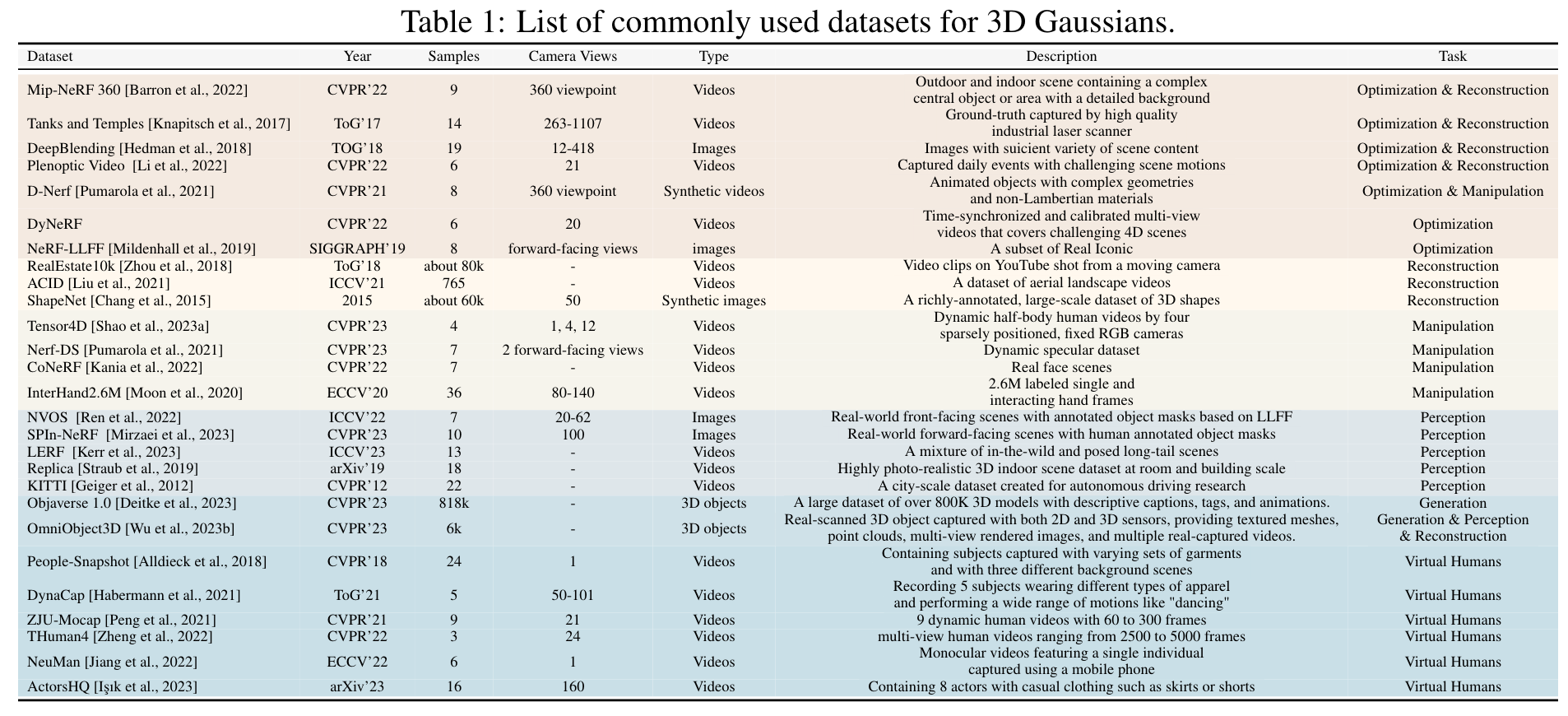
常用数据集

相关工作

对3D Gaussian相关工作进行分类：

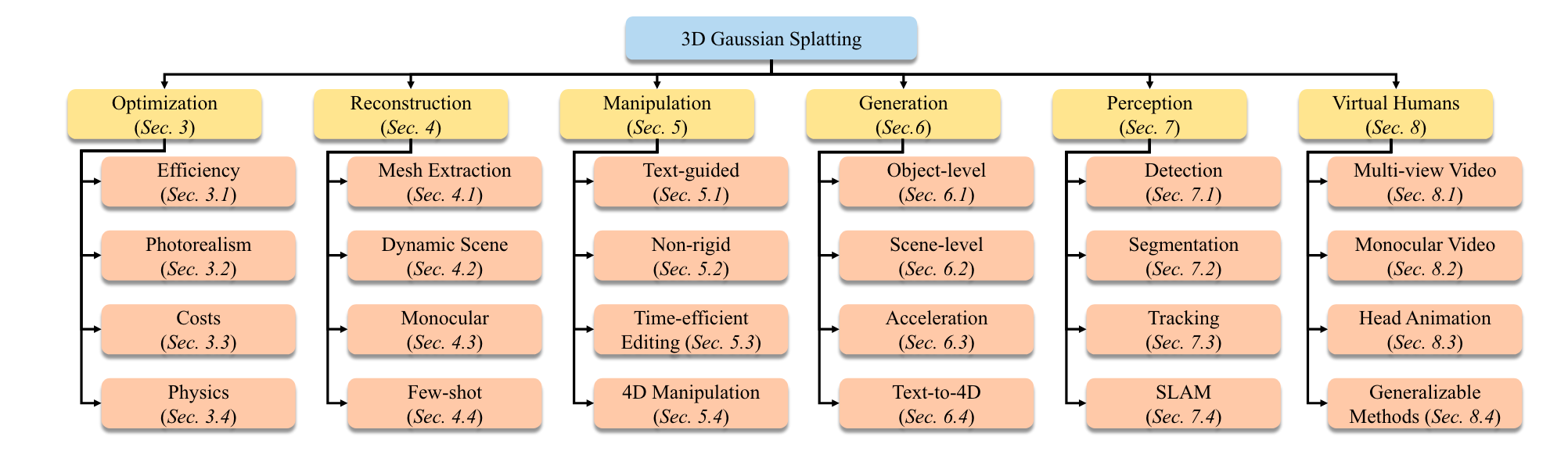
Gaussian本身的优化

  1. 在提高3DGS的内存效率
    • Scaffold-GS(CVPR2024):使用锚点来分布局部3D Gaussian，并根据视锥体内的观察方向和距离动态预测相关属性，能够做到更快收敛、更少基元和更好的视觉质量
    • Compact 3D Gaussian(CVPR2024)：Gaussian的压缩
  2. 进一步提高渲染图像的质量，解决锯齿和伪影问题
    • Mip-Splatting(CVPR2024)：借助3D平滑和2D Mip实现抗锯齿渲染
    • GaussianShader: 提出了一种在3D Gaussian上应用着色函数的方法，增强镜面特征和反射表面的场景
    • Relightable 3D Gaussian: 提出了一种新的基于点的渲染框架，用于从多视图图像中进行材质和照明分解
    • GaussianPro: 利用渐进传播策略来指导3D Gaussian的致密化，利用场景的现有重建几何形状的先验以及PatchMatch技术来生成具有准确位置和方向的新Gaussian
  3. 原始的3DGS需要大量的训练图像，降低合成新视角的图像成本则是希望能够在较少训练图像上得到优秀的场景表征
    • DepthRegGS：使用少视图来优化Gaussian，其中使用深度图(由与训练的单目模型获得)作为指导和约束
    • FSGS：少视图(3个训练视图)的实时场景视图合成
    • SparseGS: 少视图Gaussian
    • 可能改进：改进3D Gaussian的致密化方式、利用几何信息提高渲染质量
  4. 动态场景的表征
    • 4D Gaussian Splatting(CVPR2024): 基于3D Gaussian完成动态场景的表征，将空间和时间作为一个整体进行建模
    • 4D Gaussian Splatting(ICLR2024)：提出了一种用于实时3D动态场景渲染的新框架
    • DynMF：提出一种功能紧凑而高效的表达方式，将动态场景分解为若干神经轨迹
    • PhysGaussian(CVPR2024)：将牛顿动力学集成到3D Gaussian中，实现高质量的运动合成
    • Deformable 3D Gaussians(CVPR2024): 提出了一种可变形的3D Gaussian分布方式。该方式使用显式3D Gaussian重构场景，并通过变形场来学习处于规范空间内的Gaussian，来对单目动态场景进行建模

重建 Reconstruction

  1. 表面mesh重建：利用3D Gaussian来完成表面mesh提取
    • SuGaR(CVPR2024)：结合正则项来促进高斯和场景表面之间的对齐，然后使用泊松重建从高斯中导出mesh网格
    • NeuSG：引入尺度正则化器，通过强制3D Gaussian变得非常薄，将其中心拉近表面
    • 可能改进：对于表面网格提取，引入光照分解的方法可能可以提取更真实的表面纹理
  2. Few-shot重建：从少量图片中重建3D场景，要求模型具有泛化性
    • pixelSplat：从两个输入视图来推断3D Gaussian场景
    • TriplaneGaussian:使用混合表示来从单视图中重建3D场景，该混合表示结合了显示的点云和隐式的三平面场
    • Splatter Image(CVPR2024):一种非常快速的单目3D对象重建方法

Gaussian的编辑和操作

  • GaussianEditor(CVPR2024)：一种基于3D Gaussian的3D编辑算法
  • Control4D(CVPR2024)：提出了一种使用文本指令来编辑4D肖像的框架
  • SC-GS(CVPR2024): 提出了一种新的表示，将动态场景的运动和外观分别显式地分解为稀疏控制点和密集高斯
  • CoGS：一种可控的Gaussian Splatting方法，可以直接操纵场景元素，提供动态场景的实时控制

生成 Generation

  • GaussianDreamer(CVPR2024): 提出一种快速的3D对象生成框架，通过3D Gaussian来连接2D和3D扩散模型，可以在短时间内生成高质量的3D实例
  • GSGEN(CVPR2024): 使用3D Gaussian来完成文本到3D对象的生成
  • AGG: 设计了一种级联的生成pipeline，可以做到泛化性地物体生成，无需针对每个实例进行优化
  • LucidDreamer(CVPR2024): 提出一种称为Interval Score Matching(ISM)的方法，解决了SDS(Score Distillation Sampling)会带来的过度平滑的问题
  • DreamGaussian(ICLR2024): 基于3D Gaussian的3D内容生成框架
  • Align Your Gaussians: 允许生成动态的3D内容
  • 4DGen: 使用静态3D资源和单目视频序列来构建4D内容
  • DreamGaussian4D: 在Gaussian Splatting中显式建模空间变换来完成图像到4D的生成
  • Efficient4D: 利用视频来生成4D对象

感知 Perception

  1. Open-vocabulary semantic object detection and localization：开放词汇语义对象检测和定位
    • LEGaussians(CVPR2024): 提出了Language Embedded 3D Gaussian，一种用于开放词汇查询任务的新颖场景表示
    • FMGS: 集成了用于Language Embedding的多分辨率hash encoding以及用于场景表征的3D Gaussian
  2. 3D Segmentation
  3. Tracking：动态物体的跟踪
  4. SLAM

虚拟人 Virtual Humans

  • Human Gaussian Splatting: 利用3D Gaussian，从多视图视频中学习逼真的人体头像
  • HUGS: Human Gaussian Splats: 利用单目视频来重建人体和静态背景
  • Human101: 利用单目视频完成快速重建和实时渲染
  • 3DGS-Avatar(CVPR2024): 利用单目视频，来分别建模人体以及布料变形，训练时间短，交互式渲染帧率高
  • GaussianAvatar(CVPR2024): 使用3D Gaussian来联合优化运动和外观
  • GauHuman: 从SMPL的LBS权重开始，使用有效的姿态细化模块来纠正SMPL姿态
  • GaussianAvatars(CVPR2024): 将3D Gaussian绑定到参数化可形变面部模型上，在表情、姿式和视角方面完全可控
  • HeadGaS: 利用3D Gaussian来进行3D头部动态重建
  • PSAvatar: 使用基于点的可变形形状模型，不仅可以重建面部结构，还可以重建复杂的几何形状，例如眼镜和发型等
  • Gaussian Head Avatar(CVPR2024): 使用3D Gaussian以及基于MLP的变形场来进行头部重建，避免了LBS的有限表达能力

改进方向/Feature

  1. 处理3D Gaussian中的漂浮元素(Floating Elements)：通过透明度阈值过滤Gaussian/增加正则项使得这些Floating Elements靠近表面
  2. mech重建：如何利用3D Gaussian来增强或者补充其他的多视图重建技术
  3. 渲染的真实性：考虑结合MVS等方法，提高几何精度
  4. 实时渲染：进一步提高3D Gaussian渲染的速度
  5. 少样本3D Gaussian：如何利用少样本来学习3D Gaussian
  6. 镜面反射与非镜面反射区域的区分
  7. 生成更加具有真实性的3D对象和场景
  8. 将大模型(例如LLM、SAM等)与3D Gaussian进行集成
  9. 将3D Gaussian作为工具来完成其他相关任务
深度学习 > 3D视觉
#3D #论文笔记 #3D Gaussian
3D Gaussian介绍以及综述
http://example.com/2024/03/12/3D-Gaussian介绍以及综述/
作者
EverNorif
发布于
2024年3月12日
许可协议