3D Gaussian相关工作介绍(1)

GaussianPro(ICML2024)

原始的3D Gaussians在很大程度上依赖SfM生成的初始化点云，但是SfM在处理无纹理表面的时候，通常无法产生足够的初始化点，从而导致后续的流程受到影响。另外，原始3D Gaussians的致密化策略也较为简单，仅在梯度上进行Gaussians的致密，而没有考虑到场景的几何。这些问题最终会导致在一些无纹理的区域Gaussians分布较少，最终降低渲染质量。

GaussianPro(ICML2024)则提出融合传统MVS中的Patch Match技术，使用渐进式传播策略来指导3D Gaussians进行致密化。这种方式能够逐步产生具有准确位置和方向的Gaussian。

模型架构

下面这张图概述了GaussiansPro的整个Pipeline。

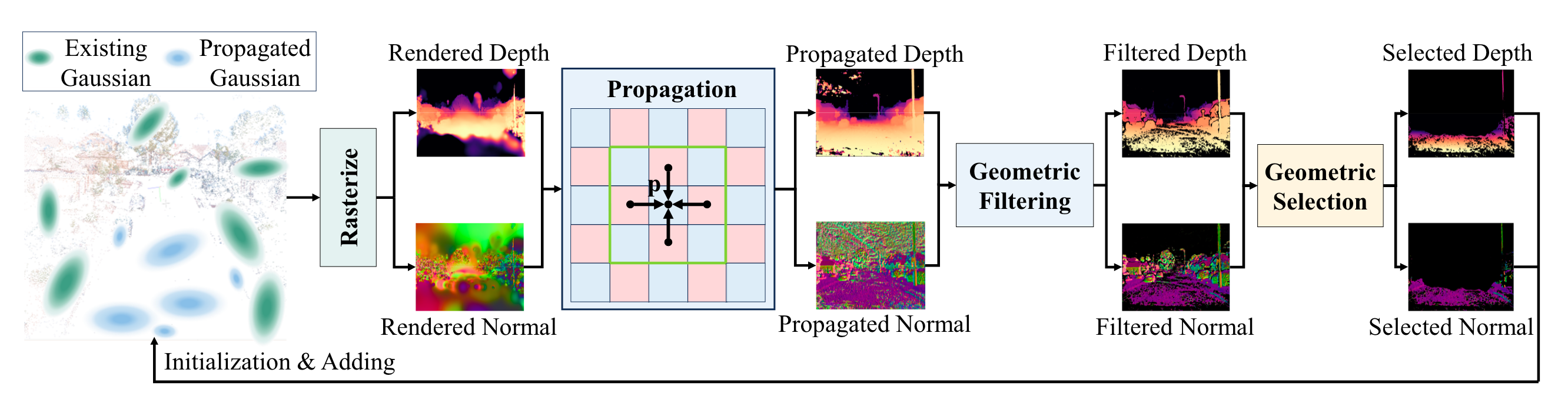
假设场景中已经有了一部分的Gaussians，无论是通过SfM初始化得到的，还是经过了一段时间的优化得到的，我们考虑的是如何进行新Gaussians的添加。

合理的Gaussians致密化应该遵循一定的几何约束，例如在局部平面上进行Gaussian的增长。但是由于3D Gaussians的离散分布与不规则的拓扑形状，不方便做到几何形状的感知，因此也很难在局部表面上搜索相邻Gaussians分布。GaussianPro将该问题转化到2D上来进行，它的核心思想在于，如果Gaussian位于3D空间的同一局部平面上，那么它们的2D投影应该也位于相邻区域，并且表现出相似的几何属性，例如深度和法线。

对于每张输入视图，我们首先可以通过alpha混合的方式来渲染出对应视角下的深度和法线图，称为渲染深度图和渲染法线图。其中，深度的累积对应的是通过坐标转换之后得到的齐次坐标的最后一维，法线则对应的是每个3D Gaussian椭球最短轴的方向。

现在我们有了给定视角下渲染的深度图和法线图，对于其中的每个像素\(p\)，我们都可以得到它对应的一个3D局部平面。这个3D局部平面可以通过深度\(d\)和法线\(\mathbf{n}\)来表示，法线\(\mathbf{n}\)就是渲染法线图中的法线方向，深度\(d\)表示相机坐标系原点到该局部平面的距离，计算如下： \[ d = z \mathbf{n}^T \mathbf{K}^{-1} \widetilde{p} \] 其中，z表示渲染深度图中该像素对应的值，\(\mathbf{K}\)表示相机内参，\(\widetilde{p}\)表示像素\(p\)的齐次坐标。

考虑到相邻的像素可能会共享相似的深度和法线值，所以对于每个像素，我们迭代地将其相邻像素的深度和法线值传播到该像素，以此得到一组候选值。对于这些候选值，则采用经典的PatchMatch技术来选择其中满足多视图光度一致性的最佳候选，将其传播到该像素上，得到的图称为传播深度图和传播法线图。

具体来说，对于该视角下的每个像素，我们都可以得到一组候选值，即深度和法线值，以此为基础可以得到一个局部平面的参数。每个候选值都对应一个局部平面，基于这个局部平面，我们可以将RGB图下的该像素投影到相邻视图上，得到在相邻视图上该像素对应的颜色，这个过程是通过单应变换完成的。最终，我们选择具有最佳颜色一致性的候选平面作为更新后深度和法线值。迭代进行多次传播\(u(=3)\)次，以此来做到在大范围内的信息传递。

在传播过程中不可避免会出现错误，因此还使用使用几何一致性来过滤掉不可靠的传播深度和传播法线，得到过滤后的结果。

对比渲染深度图和传播深度图，它们之间会存在像素上的差异。那些有着较大差异(超过阈值\(\sigma\))的像素，则意味着现有的3D Gaussians可能无法准确捕获真实的几何形状，还需要增加更多的Gaussian。因此我们将该像素反向投影到3D空间中，并将其初始化为新的Gaussian。

此外，GaussianPro还提出了一个平面约束，鼓励Gaussian的形状贴近真实表面。

该约束首先强制渲染法线与传播法线之间具有一致性，得到\(L_{normal}\)： \[ L_{normal} = \sum_{p\in \mathcal{Q}} || \widehat{N}(p) - \overline{N}(p)||_1 + || 1 - \widehat{N}(p)^T \overline{N}(p) ||_1 \] 其中\(\widehat{N}\)表示渲染法线图，\(\overline{N}\)表示传播法线图，\(\mathcal{Q}\)表示经过几何一致性过滤之后的有效像素。

以及为了确保Gaussian的最短轴能够代表法线方向，GaussianPro还参考NeuSG引入了尺度正则化损失\(L_{scale}\)，该损失能够将Gaussian的最小尺度限制为接近于0，有效地将Gaussian平坦化为接近平面形状。最终的平面约束损失是这两个损失的综合： \[ L_{planar} = \beta L_{normal} + \gamma L_{scale} \] 上述就是GaussianPro的所有Pipeline。在实际训练的时候，大部分流程与原始3D Gaussian相同。不过除了原始的致密化操作之外，GaussianPro每\(m(=50)\)轮迭代进行一次渐进传播，并进行新Gaussian的添加。

简单总结

GaussianPro将PatchMatch思想融入3D Gaussians中，以此改进Gaussian的致密化操作。它以渲染出来的深度图和法线图为基础进行渐进传播，得到传播后的深度图和法线图，并以两者的差异为标准进行新Gaussian的添加。此外，它还引入了平面约束，鼓励Gaussian的形状更加贴近真实表面。

GaussianPro的项目地址为kcheng1021/GaussianPro

GaussianGrouping

Gaussian Grouping完成的任务是进行基于3D Gaussian的场景分割以及编辑，它主要通过扩展3D Gaussian上的id属性特征，利用SAM提供Mask监督来完成。主要思想就是将每个Gaussian进行分类，然后基于分类的结果进行编辑，包括3D对象的删除、修复、着色以及场景重组。

模型架构

GaussianGrouping整体的Pipeline如下所示：

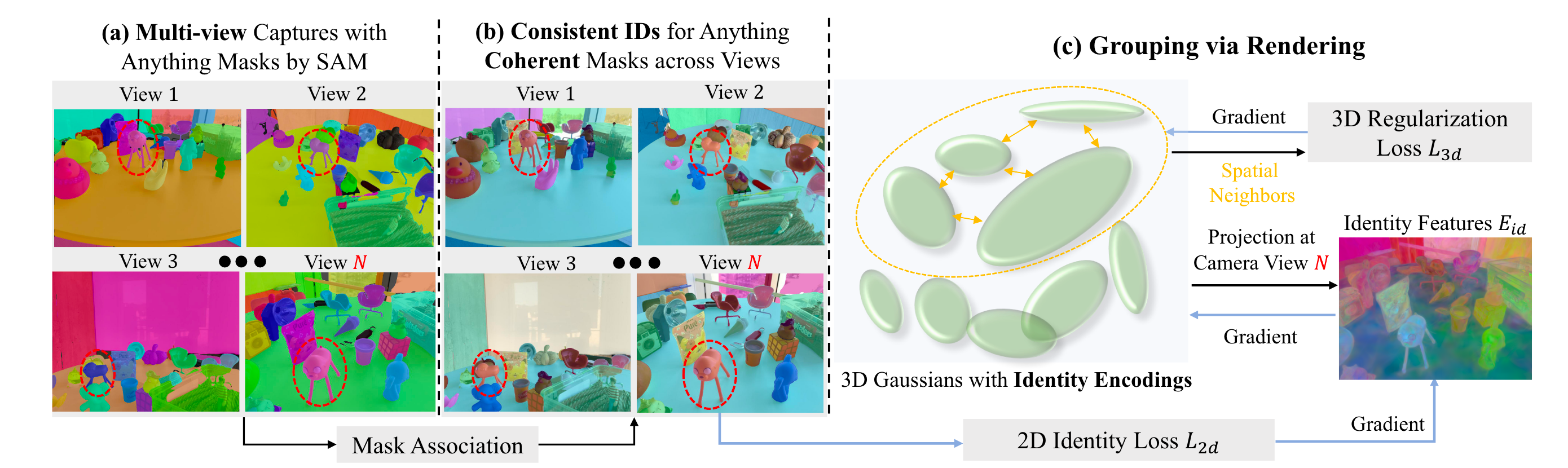
首先，对于训练场景的多视角图片，采用SAM的Everything Mode来提取出Mask图，图片中的每个像素都被赋予一个Mask id。不过由于不同图像之间是独立的，Mask id也是相互独立的。要想用来指导训练，则需要统一对齐不同Mask图之间的id。GaussianGrouping将多视图Mask图看作是一系列视频帧，然后采用预训练的zero-shot tracker DEVA来进行Tracking，从而统一多视图之间的Mask id。

之后，GaussianGrouping为每个Gaussian扩展一个Identity属性，这是一个特征向量(维度=16)，该特征表征Gaussian的分类结果，可以视作是分割特征。对该特征进行光栅化渲染，则可以得到对应的分割特征图。该分割特征图经过一个MLP之后，则可以得到预测的ID图，该ID图由前面得到的Mask图进行监督，计算交叉熵作为损失函数。

除了交叉熵损失之外，GaussianGrouping还引入了一个3D正则化损失来进一步提高Gaussian分组的精度。该损失的主要思想是利用3D空间上的一致性，强制每个Gaussian与跟他最近的k个Gaussian具有相似的分割特征。在原始3D Gaussian的Pipeline上增加分割相关处理，就可以训练得到一个具备分割特征的3D Gaussian。

有了训练好的3D Gaussian之后，就可以进行场景相关的编辑，包括：

• 3D对象删除：删除目标对应的Gaussian
• 3D场景重新合成：交换不同场景之间相应的Gaussian
• 3D对象着色/风格迁移：调整对象相应Gaussian的颜色属性(球谐函数)
• 3D对象修复：在删除了3D对象之后，可能会造成遮挡的空洞，3D对象修复就是希望能够填补这部分空洞，使得结果更加自然和逼真
  • 首先删除相关的3D Gaussian，然后找到删除后会出现空洞的训练视图，利用图片修复模型LAMA进行修复和填充
  • 添加新的Gaussian，然后利用修复后的训练图片来训练该部分新添加的Gaussian

简单总结

GaussianGrouping在每个Gaussian上扩展一个Identity特征作为分割依据，然后使用SAM对多视图进行分割得到Mask图，利用zero-shot tracker进行Mask图之间的对齐，然后利用这些Mask图来监督Identity特征的学习。完成GaussianGrouping完成分割特征学习之后，就可以基于分割结果就能进行相关场景编辑。

GaussianGrouping还提供了LERF-Mask dataset数据集，其中手工注释了LERF三个场景的Mask。

GaussianGrouping的项目地址为：[lkeab/gaussian-grouping